1
GATE ME 2016 Set 3
Numerical
+2
-0
A firm uses a turning center, a milling center and a grinding machine to produce two parts. The table below provides the
machining time required for each part and the maximum machining time available on each machine. The profit per unit on parts $${\rm I}$$ and $${\rm II}$$ are Rs. $$40$$ and Rs. $$100,$$ respectively. The maximum profit per week of the firm is Rs. _______________
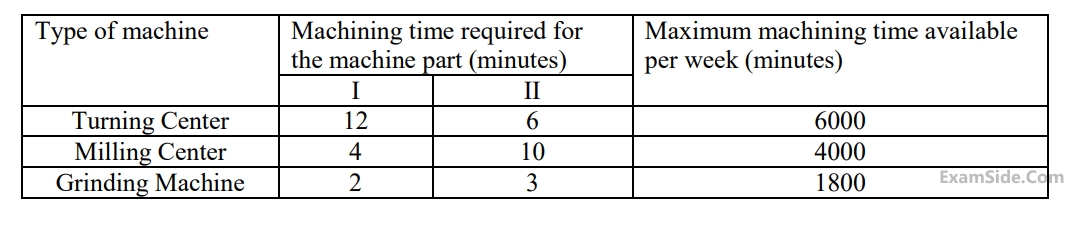

Your input ____
2
GATE ME 2015 Set 3
MCQ (Single Correct Answer)
+2
-0.6
For the linear programming problem:
$$\eqalign{ & Maximize\,\,\,\,\,Z = 3{x_1} + 2{x_2} \cr & Subject\,\,to\,\,\,\, - 2{x_1} + 3{x_2} \le 9 \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{x_1} - 5{x_2} \ge - 20 \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{x_1},\,\,{x_2} \ge 0 \cr} $$
$$\eqalign{ & Maximize\,\,\,\,\,Z = 3{x_1} + 2{x_2} \cr & Subject\,\,to\,\,\,\, - 2{x_1} + 3{x_2} \le 9 \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{x_1} - 5{x_2} \ge - 20 \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{x_1},\,\,{x_2} \ge 0 \cr} $$
The above problem has
3
GATE ME 2014 Set 3
Numerical
+2
-0
Consider an objective function $$Z\left( {{x_1},{x_2}} \right) = 3{x_1} + 9{x_2}$$ and the constraints
$$\eqalign{ & {x_1} + {x_2} \le 8, \cr & {x_1} + 2{x_2} \le 4, \cr & {x_1} \ge 0,{x_2} \ge 0, \cr} $$
$$\eqalign{ & {x_1} + {x_2} \le 8, \cr & {x_1} + 2{x_2} \le 4, \cr & {x_1} \ge 0,{x_2} \ge 0, \cr} $$
The maximum value of the objective function is ________________.
Your input ____
4
GATE ME 2013
MCQ (Single Correct Answer)
+2
-0.6
A linear programming problem is shown below.
$$\eqalign{ & Maximize\,\,\,\,3x + 7y \cr & Subject\,\,to\,\,\,3x + 7y \le 10 \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,4x + 6y \le 8 \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x,\,\,y \ge 0 \cr} $$
$$\eqalign{ & Maximize\,\,\,\,3x + 7y \cr & Subject\,\,to\,\,\,3x + 7y \le 10 \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,4x + 6y \le 8 \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x,\,\,y \ge 0 \cr} $$
It has ..............
Questions Asked from Linear Programming (Marks 2)
Number in Brackets after Paper Indicates No. of Questions
GATE ME Subjects
Engineering Mechanics
Machine Design
Strength of Materials
Heat Transfer
Production Engineering
Industrial Engineering
Turbo Machinery
Theory of Machines
Engineering Mathematics
Fluid Mechanics
Thermodynamics
General Aptitude