1
GATE ECE 2006
MCQ (Single Correct Answer)
+2
-0.6
Let $$g\left( t \right){\mkern 1mu} {\mkern 1mu} \,\,\,\,\,{\mkern 1mu} = {\mkern 1mu} {\mkern 1mu} p\left( t \right){}^ * p\left( t \right)$$ where $$ * $$ denotes convolution and $$p(t) = u(t) - u(t-1)$$ with $$u(t)$$ being the unit step function
The impulse response of filter matched to the signal $$s(t) = g(t)$$ $$ - \delta {\left( {t - 2} \right)^ * }\,\,g\left( t \right)$$ is given as:
2
GATE ECE 2006
MCQ (Single Correct Answer)
+2
-0.6
In the following figure the minimum value of the constant “C”, which is to be added to y1(t) such that y1(t) and y2(t) are different, is
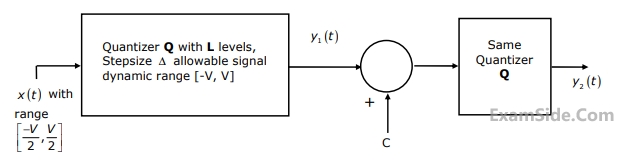

3
GATE ECE 2005
MCQ (Single Correct Answer)
+2
-0.6
A symmetric three-level midtread quantizer is to be designed assuming equiprobable occurrence of all quantization levels.
The quantization noise power for the quantization region between –a and +a in the figure is
4
GATE ECE 2005
MCQ (Single Correct Answer)
+2
-0.6
A symmetric three-level midtread quantizer is to be designed assuming equiprobable occurrence of all quantization levels.
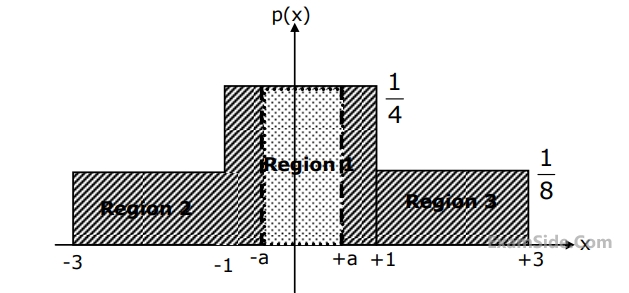
If the input probability density function is divided into three regions as shown in figure, the value of 'a' in the figure is

Questions Asked from Noise In Digital Communication (Marks 2)
Number in Brackets after Paper Indicates No. of Questions
GATE ECE 2025 (1)
GATE ECE 2016 Set 1 (2)
GATE ECE 2015 Set 2 (1)
GATE ECE 2015 Set 1 (2)
GATE ECE 2014 Set 4 (2)
GATE ECE 2014 Set 2 (1)
GATE ECE 2013 (1)
GATE ECE 2012 (2)
GATE ECE 2011 (2)
GATE ECE 2010 (2)
GATE ECE 2009 (2)
GATE ECE 2008 (1)
GATE ECE 2007 (5)
GATE ECE 2006 (2)
GATE ECE 2005 (3)
GATE ECE 2004 (1)
GATE ECE 2003 (2)
GATE ECE 2001 (1)
GATE ECE 1999 (2)
GATE ECE 1988 (2)
GATE ECE 1987 (1)
GATE ECE Subjects
Network Theory
Control Systems
Electronic Devices and VLSI
Analog Circuits
Digital Circuits
Microprocessors
Signals and Systems
Representation of Continuous Time Signal Fourier Series Fourier Transform Continuous Time Signal Laplace Transform Discrete Time Signal Fourier Series Fourier Transform Discrete Fourier Transform and Fast Fourier Transform Discrete Time Signal Z Transform Continuous Time Linear Invariant System Discrete Time Linear Time Invariant Systems Transmission of Signal Through Continuous Time LTI Systems Sampling Transmission of Signal Through Discrete Time Lti Systems Miscellaneous
Communications
Electromagnetics
General Aptitude