1
GATE ECE 2016 Set 1
MCQ (Single Correct Answer)
+2
-0.6
An analog pulse s(t) is transmitted over an additive white Gaussian noise (AWGN) channel. The received signal is r(t) = s(t) + n(t), where n(t) is additive white Gaussian noise with power spectral density $${{{N_0}} \over 2}$$. The received signal is passed through a filter with impulse response h(t). Let $${E_s}$$ and $${E_n}$$ denote the energies of the pulse s(t) and the filter h(t), respectively. When the signal-to-noise ratio (SNR) is maximized at the output of the filter $$\left( {SN{R_{\max }}} \right)$$, which of the following holds?
2
GATE ECE 2016 Set 1
Numerical
+2
-0
A digital communication system uses a repetition code for channel encoding/decoding. During transmission, each bit is repeated three times (0 is transmitted as 000, and 1 is transmitted as 111). It is assumed that the source puts out symbols independently and with equal probability. The decoder operates as follows: In a block of three received bits, if the number of zeros exceeds the number of ones, the decoder decides in favor of a 0, and if the number of ones exceeds the number
of zeros, the decoder decides in favor of a 1, Assuming a binary symmetric channel with crossover probability p = 0.1, the average probability of error is _______
Your input ____
3
GATE ECE 2015 Set 2
MCQ (Single Correct Answer)
+2
-0.6
Consider a binary, digital communication system which uses pulses g (t) and − g (t)for transmitting bits over an AWGN channel. If the receiver uses a matched filter, which one of the following pulses will give the minimum probability of bit error?
4
GATE ECE 2015 Set 1
Numerical
+2
-0
The input X to the Binary Symmetric Channel (BSC) shown in the figure is ‘1’ with probability 0.8. The cross-over probability is 1/7. If the received bit Y = 0, the conditional probability that ‘1’ was transmitted is _______.
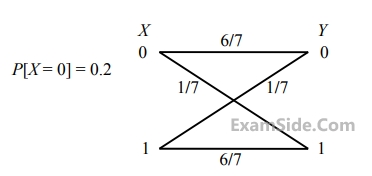

Your input ____
Questions Asked from Noise In Digital Communication (Marks 2)
Number in Brackets after Paper Indicates No. of Questions
GATE ECE 2025 (1)
GATE ECE 2016 Set 1 (2)
GATE ECE 2015 Set 2 (1)
GATE ECE 2015 Set 1 (2)
GATE ECE 2014 Set 4 (2)
GATE ECE 2014 Set 2 (1)
GATE ECE 2013 (1)
GATE ECE 2012 (2)
GATE ECE 2011 (2)
GATE ECE 2010 (2)
GATE ECE 2009 (2)
GATE ECE 2008 (1)
GATE ECE 2007 (5)
GATE ECE 2006 (2)
GATE ECE 2005 (3)
GATE ECE 2004 (1)
GATE ECE 2003 (2)
GATE ECE 2001 (1)
GATE ECE 1999 (2)
GATE ECE 1988 (2)
GATE ECE 1987 (1)
GATE ECE Subjects
Network Theory
Control Systems
Electronic Devices and VLSI
Analog Circuits
Digital Circuits
Microprocessors
Signals and Systems
Representation of Continuous Time Signal Fourier Series Discrete Time Signal Fourier Series Fourier Transform Discrete Time Signal Z Transform Continuous Time Linear Invariant System Transmission of Signal Through Continuous Time LTI Systems Discrete Time Linear Time Invariant Systems Sampling Continuous Time Signal Laplace Transform Discrete Fourier Transform and Fast Fourier Transform Transmission of Signal Through Discrete Time Lti Systems Miscellaneous Fourier Transform
Communications
Electromagnetics
General Aptitude



