A BPSK scheme operating over an AWGN channel with noise power spectral density of N₀2, uses equi-probable signals $$${s_1}\left( t \right) = \sqrt {{{2E} \over T}\,\sin \left( {{\omega _c}t} \right)} $$$
and $$${s_2}\left( t \right) = - \sqrt {{{2E} \over T}\,\sin \left( {{\omega _c}t} \right)} $$$

over the symbol interval, $$(0, T)$$. If the local oscillator in a coherent receiver is ahead in phase by 45⁰ with respect to the received signal, the probability of error in the resulting system is

A binary symmetric channel (BSC) has a transition probability of 1/8. If the binary transmit symbol X is such that P(X =0) = 9/10, then the probability of error for an optimum receiver will be

A four phase and an eight-phase signal constellation are shown in the figure below.

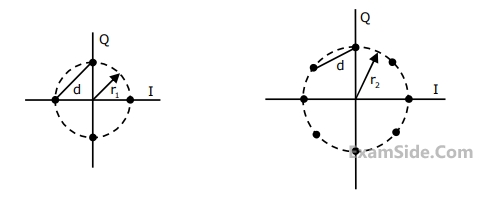
For the constraint that the minimum distance between pairs of signal points be d for both constellations, the radii r₁, and r² of the circles are

A four phase and an eight-phase signal constellation are shown in the figure below.

Assuming high SNR and that all signals are equally probable, the additional average transmitted signal energy required by the 8-PSK signal to achieve the same error probability as the 4-PSK signal is