For the digital block shown in Figure. 2(a), the output Y=f(S₃,S₂,S₁,S₀) where S₃ is MSB and S₀ is LSB. Y is given in terms of minterms as $$Y\, = \,\sum m\left( {1,5,6,7,11,12,13,15} \right)$$ and its complements $$\overline Y \, = \,\sum m\left( {0,2,3,4,8,9,10,14} \right)$$.

(a) Enter the logical values in the given Karnaugh map [figure2(b)] for the output Y.
(b) Write down the expression for Y in sum-of products from using minimum number of terms.
(c) Draw the circuit for the digital logic boxes using four 2-input NAND gates only for each of the boxes.

The operating conditions (ON = 1, OFF = 0) of three pumps (x,y,z) are to be monitored. x = 1 implies that pump X is on. It is required that the indicator (LED) on the panel should glow when a majority of the pumps fail.

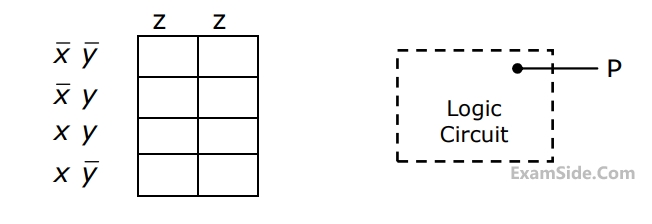
(a) Enter the logical values in the K-map in the format shown in figure 3(a). Derive the minimal Boolean sum-of-products expression whose output is zero when a majority of the pumps fail.
(b) The above expression is implemented using logic gates, and point P is the output of this circuit, as shown in figure 3(b). P is at 0 V when a majority of the pumps fails and is at 5 V otherwise. Design a circuit to drive the LED using this output. The current through the LED should be 10 mA and the voltage drop across it is 1V. Assume that P can source or sink 10 mA and a 5 V supply is available.

The truth table for the output Y in terms of three inputs A, B and C are given in table. Draw a logic circuit realization using only NOR gates.