The desired product $$X$$ can be prepared by reacting the major product of the reactions in LIST-I with one or more appropriate reagents in LIST-II (given, order of migratory aptitude: aryl > alkyl > hydrogen)


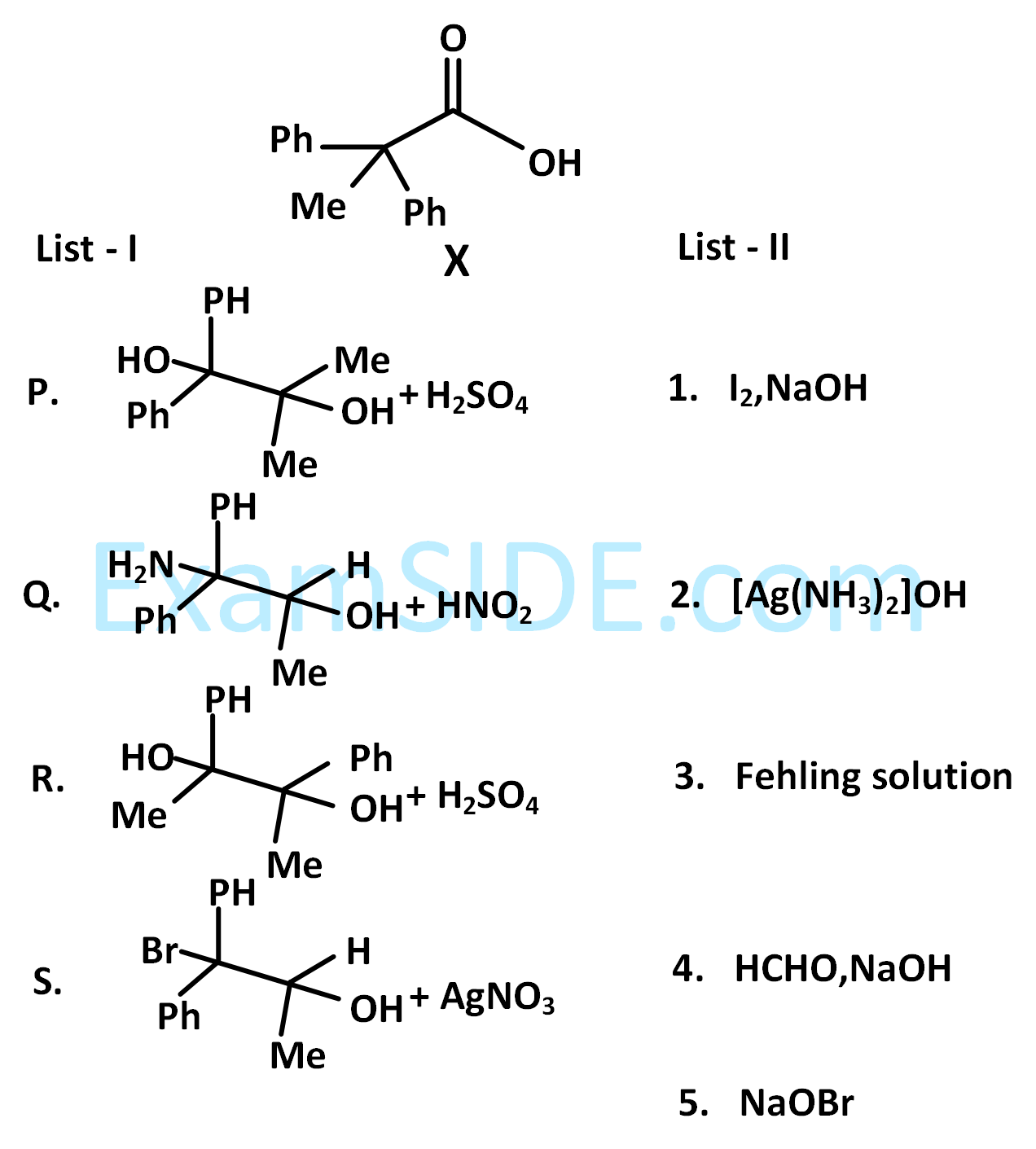
The correct option is

LIST-I contains reactions and LIST-II contains major products.



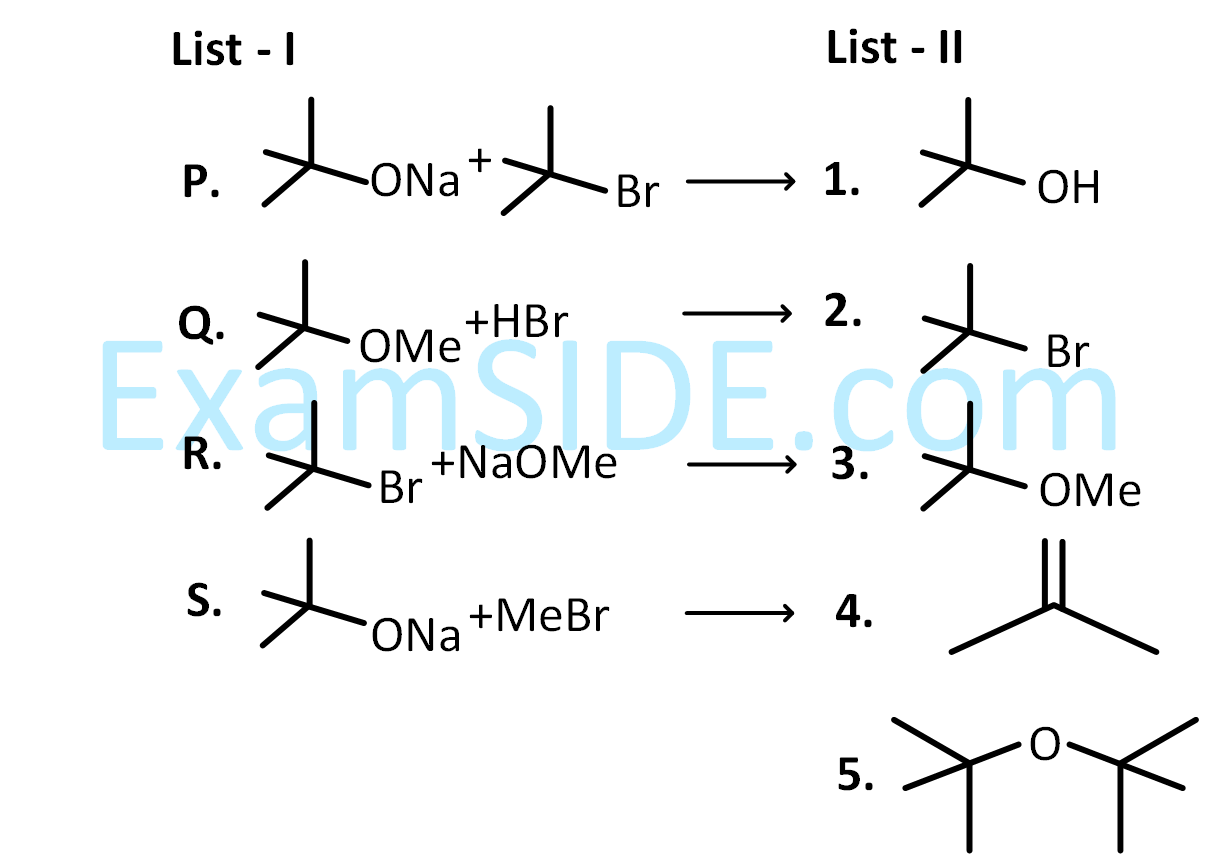
Match the reaction in LIST-I with one or more products in LIST-II and choose the correct option.

For a reaction, $$A\,\,\rightleftharpoons\,\,P,$$ the plots of $$\left[ A \right]$$ and $$\left[ P \right]$$ with time at temperature $${T_1}$$ and $${T_2}$$ are given below.


If $${T_2} > {T_1},$$ the correct statement(s) is (are) (Assume $$\Delta {H^ \circ }$$ and $$\Delta {S^ \circ }$$ are independent of temperature and ratio of $$lnK$$ at $${T_1}$$ to $$lnK$$ at $${T_2}$$ is greater than $${{{T_2}} \over {{T_1}}}.$$ Here $$H,$$ $$S,G$$ and $$K$$ are enthalpy, entropy, Gibbs energy and equilibrium constant, respectively.)

For any positive integer n, define

$${f_n}:(0,\infty ) \to R$$ as

$${f_n} = \sum\limits_{j = 1}^n {{{\tan }^{ - 1}}} \left( {{1 \over {1 + (x + j)(x + j - 1)}}} \right)$$

for all x$$ \in $$(0, $$\infty $$). (Here, the inverse trigonometric function tan^$$-$$1 x assumes values in $$\left( { - {\pi \over 2},{\pi \over 2}} \right)$$). Then, which of the following statement(s) is (are) TRUE?