Let $${f_1}:R \to R,\,{f_2}:\left( { - {\pi \over 2},{\pi \over 2}} \right) \to R,\,{f_3}:( - 1,{e^{\pi /2}} - 2) \to R$$ and $${f_4}:R \to R$$ be functions defined by

(i) $${f_1}(x) = \sin (\sqrt {1 - {e^{ - {x^2}}}} )$$,

(ii) $${f_2}(x) = \left\{ \matrix{ {{|\sin x|} \over {\tan { - ^1}x}}if\,x \ne 0,\,where \hfill \cr 1\,if\,x = 0 \hfill \cr} \right.$$

the inverse trigonometric function tan^$$-$$1x assumes values in $$\left( { - {\pi \over 2},{\pi \over 2}} \right)$$,

(iii) $${f_3}(x) = [\sin ({\log _e}(x + 2))]$$, where for $$t \in R,\,[t]$$ denotes the greatest integer less than or equal to t,

(iv) $${f_4}(x) = \left\{ \matrix{ {x^2}\sin \left( {{1 \over x}} \right)\,if\,x \ne 0 \hfill \cr 0\,if\,x = 0 \hfill \cr} \right.$$

LIST-I	LIST-II
P. The function $$ f_1 $$ is	1. NOT continuous at $$ x = 0 $$
Q. The function $$ f_2 $$ is	2. continuous at $$ x = 0 $$ and NOT differentiable at $$ x = 0 $$
R. The function $$ f_3 $$ is	3. differentiable at $$ x = 0 $$ and its derivative is NOT continuous at $$ x = 0 $$
S. The function $$ f_4 $$ is	4. differentiable at $$ x = 0 $$ and its derivative is continuous at $$ x = 0 $$

A particle, of mass $${10^{ - 3}}$$ $$kg$$ and charge $$1.0$$ $$C,$$ is initially at rest. At time $$t=0,$$ the particle comes under the influence of an electric field $$\overrightarrow E \left( t \right) = {E_0}\sin \,\,$$ $$\omega t\widehat i,$$ where $${E_0} = 1.0\,N{C^{ - 1}}$$ and $$\omega = 10{}^3\,rad\,{s^{ - 1}}.$$ Consider the effect of only the electrical force on the particle. Then the maximum speed, in $$m{s^{ - 1}},$$ attained by the particle at subsequent times is _______________.

Consider a thin square plate floating on a viscous liquid in a large tank. The height $$h$$ of the liquid in the tank is much less than the width of the tank. The floating place is pulled horizontally with a constant velocity $${\mu _{0.}}$$ Which of the following statements is (are) true?

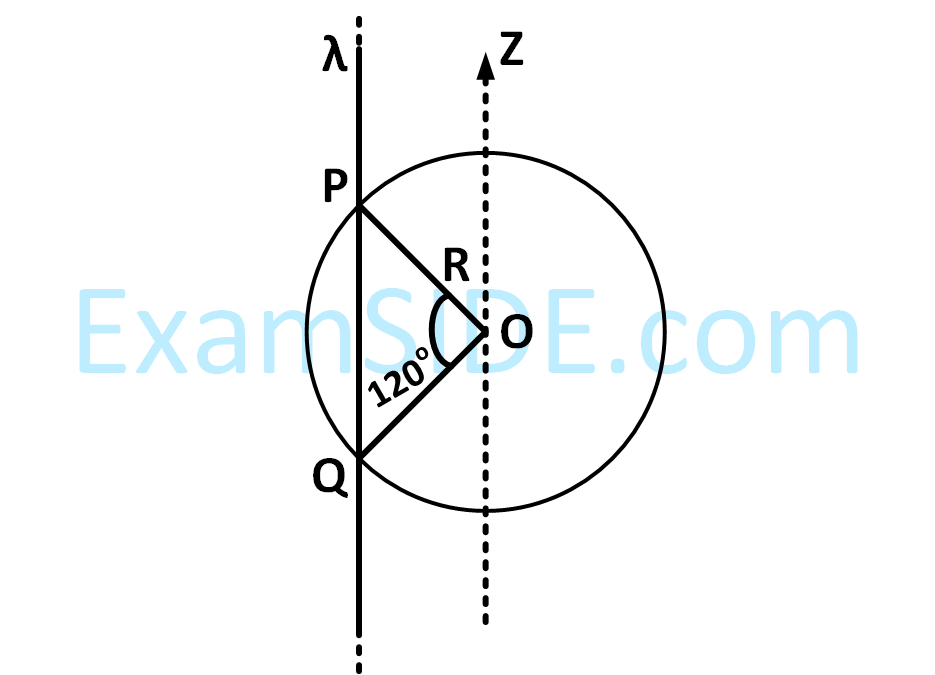
An infinitely long thin non-conducting wire is parallel to the $$z$$-axis and carries a uniform line charge density $$\lambda .$$ It pierces a thin non-conducting spherical shell of radius $$R$$ in such a way that the arc $$PQ$$ subtends an angle $${120^ \circ }$$ at the center $$O$$ of the spherical shell, as shown in the figure. The permittivity of free space is $${ \in _0}.$$ Which of the following statement is (are) true?