The electric field $$E$$ is measured at a point $$P(0,0,d)$$ generated due to various charge distributions and the dependence of $$E$$ on $$d$$ is found to be different for different charge distributions. List-$${\rm I}$$ contains different relations between $$E$$ and $$d$$. List-$${\rm II}$$ describes different electric charge distributions, along with their locations. Match the functions in List-$${\rm I}$$ with the related charge distributions in List-$${\rm II}$$.

LIST - I		LIST - II
P.	$$E$$ is independent of $$d$$	1.	A point charge Q at the origin
Q.	$$E\, \propto \,1/d$$	2.	A small dipole with point charges $$Q$$ at $$\left( {0,0,l} \right)$$ and $$-Q$$ at $$\left( {0,0, - l} \right).$$ Take $$2l < < d$$
R.	$$E\, \propto \,1/{d^2}$$	3.	An infinite line charge coincident with the x-axis, with uniform linear charge density $$\lambda $$
S.	$$E\, \propto \,1/{d^3}$$	4.	Two infinite wires carrying uniform linear charge density parallel to the $$x$$-axis. The one along $$\left( {y = 0,z = l} \right)$$ has a charge density $$ + \lambda $$ and the one along $$\left( {y = 0,z = - l} \right)$$ has a charge density Take
		5.	Infinite plane charge coincident with the $$xy$$-plane with uniform surface charge density

One mole of a monatomic ideal gas undergoes four thermodynamic processes as shown schematically in the $$PV$$-diagram below. Among these four processes, one is isobaric, one is isochoric, one is isothermal and one is adiabatic. Match the processes mentioned in List-I with the corresponding statements in List-II.

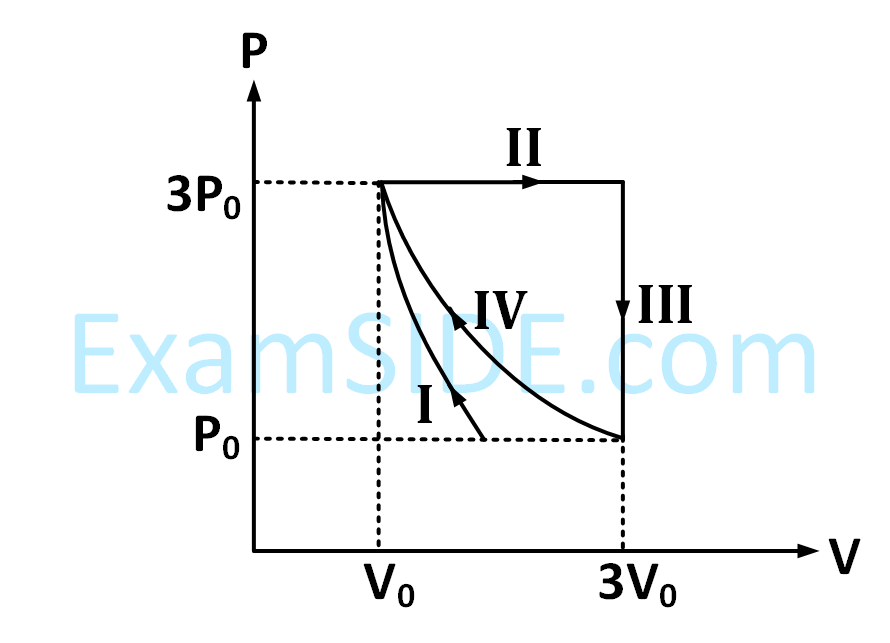
LIST - I		LIST - II
P.	In process I	1.	Work done by the gas is zero
Q.	In process II	2.	Temperature of the gas remains unchanged
R.	In process III	3.	No heat is exchanged between the gas and its surroundings
S.	In process IV	4.	Work done by the gas is 6P0V0

In the List-$${\rm I}$$ below, four different paths of a particle are given as functions of time. In these functions, $$\alpha $$ and $$\beta $$ are positive constants of appropriate dimensions and $$\alpha \ne \beta $$ In each case, the force acting on the particle is either zero or conservative. In List-$${\rm I}{\rm I}$$, five physical quantities of the particle are mentioned $$\overrightarrow p $$ is the linear momentum, $$\overrightarrow L $$ is the angular momentum about the origin, $$K$$ is the kinetic energy, $$U$$ is the potential energy and $$E$$ is the total energy. Match each path in List-$${\rm I}$$ with those quantities in List-$${\rm II}$$, which are conserved for that path.

LIST - I		LIST - II
P.	$$\overrightarrow r $$(t)=$$\alpha $$ $$t\,\widehat i + \beta t\widehat j$$	1.	$$\overrightarrow p $$
Q.	$$\overrightarrow r \left( t \right) = \alpha \cos \,\omega t\,\widehat i + \beta \sin \omega t\,\widehat j$$	2.	$$\overrightarrow L $$
R.	$$\overrightarrow r \left( t \right) = \alpha \left( {\cos \omega t\,\widehat i + \sin \omega t\widehat j} \right)$$	3.	K
S.	$$\overrightarrow r \left( t \right) = \alpha t\,\widehat i + {\beta \over 2}{t^2}\widehat j$$	4.	U
		5.	E

A particle of mass $$m$$ is initially at rest at the origin. It is subjected to a force and starts moving along the $$x$$-axis. Its kinetic energy $$K$$ changes with time as $$dK/dt = \gamma t,$$ where $$\gamma $$ is a positive constant of appropriate dimensions. Which of a positive constant of appropriate dimensions. Which of the following statement is (are) true?