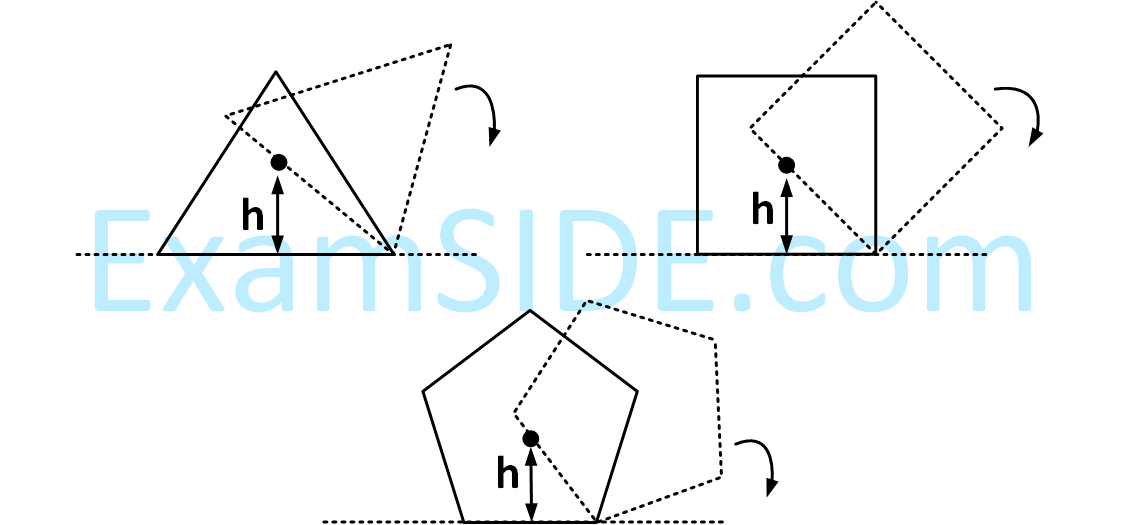
Consider regular polygons with number of sides $$n=3,4,5....$$ as shown in the figure. The center of mass of all the polygons is at height $$h$$ from the ground. They roll on a horizontal surface about the leading vertex without slipping and sliding as depicted. The maximum increase in height of the locus of the center of mass for each polygon is $$\Delta $$. Then $$\Delta $$ depends on $$n$$ and $$h$$ as

One twirls a circular ring (of mass M and radius R) near the tip of one's finger as shown in Figure 1. In the process the finger never loses contact with the inner rim of the ring. The finger traces out the surface of a cone, shown by the dotted line. The radius of the path traced out by the point where the ring and the finger is in contact is r. The finger rotates with an angular velocity $$\omega$$₀. The rotating ring rolls without slipping on the outside of a smaller circle described by the point where the ring and the finger is in contact (Figure 2). The coefficient of friction between the ring and the finger is $$\mu$$ and the acceleration due to gravity is g.

The total kinetic energy of the ring is

One twirls a circular ring (of mass M and radius R) near the tip of one's finger as shown in Figure 1. In the process the finger never loses contact with the inner rim of the ring. The finger traces out the surface of a cone, shown by the dotted line. The radius of the path traced out by the point where the ring and the finger is in contact is r. The finger rotates with an angular velocity $$\omega$$₀. The rotating ring rolls without slipping on the outside of a smaller circle described by the point where the ring and the finger is in contact (Figure 2). The coefficient of friction between the ring and the finger is $$\mu$$ and the acceleration due to gravity is g.

The minimum value of $$\omega$$₀ below which the ring will drop down is

A frame of the reference that is accelerated with respect to an inertial frame of reference is called a non-inertial frame of reference. A coordinate system fixed on a circular disc rotating about a fixed axis with a constant angular velocity $$\omega$$ is an example of a non-inertial frame of reference. The relationship between the force $$\overrightarrow F $$_rot experienced by a particle of mass m moving on the rotating disc and the force $$\overrightarrow F $$_in experienced by the particle in an inertial frame of reference is,

$$\overrightarrow F $$_rot = $$\overrightarrow F $$_in + 2m ($$\overrightarrow v $$_rot $$\times$$ $$\overrightarrow \omega $$) + m ($$\overrightarrow \omega $$ $$\times$$ $$\overrightarrow r $$) $$\times$$ $$\overrightarrow \omega $$,

where, v_rot is the velocity of the particle in the rotating frame of reference and r is the position vector of the particle with respect to the centre of the disc.


Now, consider a smooth slot along a diameter of a disc of radius R rotating counter-clockwise with a constant angular speed $$\omega$$ about its vertical axis through its centre. We assign a coordinate system with the origin at the centre of the disc, the X-axis along the slot, the Y-axis perpendicular to the slot and the Z-axis along the rotation axis ($$\omega$$ = $$\omega$$ $$\widehat k$$). A small block of mass m is gently placed in the slot at r = (R/2)$$\widehat i$$ at t = 0 and is constrained to move only along the slot.

The distance r of the block at time t is