The block diagram of a linear time invariant system is given in Figure is 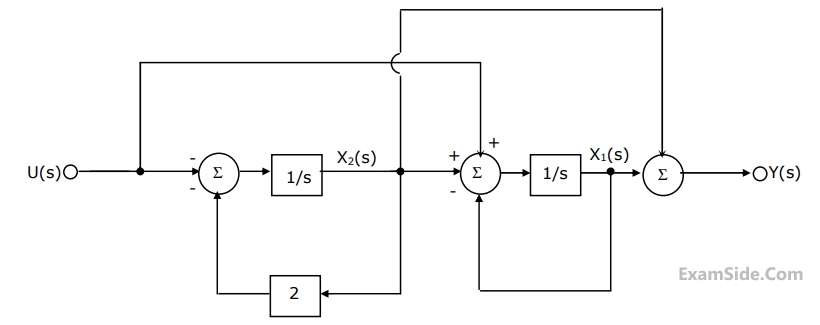(a) Write down the state variable equations for the system in matrix form assuming the state vector to be $${\left[ {{x_1}\left( t \right)\,\,{x_2}\left( t \right)} \right]^T}$$
(b) Find out the state transition matrix.
(c) Determine y(t), t ≥ 0, when the initial values of the state at time t = 0 are $${x_1}$$(0) = 1, and $${x_2}$$(0) = 1.

A certain linear, time-invariant system has the state and output representation shown below: $$$\eqalign{ & \left[ {\matrix{ {\mathop {{x_1}}\limits^ \bullet } \cr {\mathop {{x_2}}\limits^ \bullet } \cr } } \right] = \left[ {\matrix{ { - 2} & 1 \cr 0 & { - 3} \cr } } \right]\left[ {\matrix{ {{x_1}} \cr {{x_2}} \cr } } \right] + \left[ {\matrix{ 1 \cr 0 \cr } } \right]u \cr & y = \left( {\matrix{ 1 & 1 \cr } } \right)\left[ {\matrix{ {{x_1}} \cr {{x_2}} \cr } } \right] \cr} $$$
(a) Find the eigen values (natural frequencies) of the system.
(b)If u(t)=$$\delta \left( t \right)$$ and x₁(0⁺)=x₂(0⁺)=0, find x₁(t),x₂(t) and y(t), for t>0.
(c)When the input is zero, choose initial conditions $${x_1}\left( {{0^ + }} \right)$$ and $${x_2}\left( {{0^ + }} \right)$$ such that $$y\left( t \right) = A{e^{ - 2t}}$$ for t>0

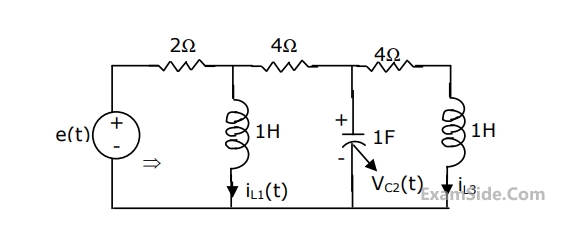
For the circuit shown in the figure, choose state variables as $${x_{1,}}{x_{2,}}{x_3}$$ to be $${i_{L1}}\left( t \right),{v_{c2}}\left( t \right),{i_{L3}}\left( t \right)$$

Wriote the state equations

$$$\left[ {\matrix{ {\mathop {{x_1}}\limits^ \bullet } \cr {\mathop {{x_2}}\limits^ \bullet } \cr {\mathop {{x_3}}\limits^ \bullet } \cr } } \right] = A\left[ {\matrix{ {{x_1}} \cr {{x_2}} \cr {{x_3}} \cr } } \right] + B\left[ {e\left( t \right)} \right]$$$

Obtain a state space representation in diagonal form for the following system $$${{{d^3}y} \over {d{t^3}}} + 6{{{d^2}y} \over {d{t^2}}} + 11{{dy} \over {dt}} + 6y = 6u\left( t \right)$$$