1
The cascode amplifier is a multistage configuration of
2
Given
$${r_d} = 20K\Omega ,\,\,{I_{DSS}}\, = \,10mA,\,\,{V_P} = - 8V$$

ID and VDS under DC conditions are respectively
3
Given the ideal operational amplifier circuit shown in figure, indicate the correct
transfer characteristics assuming ideal diodes with zero cut-in voltage.

4
The Op-Amp circuit shown in figure is a filter. The type of filter and its cut-off
frequency are respectively.

5
The voltage e
0 indicated in the figure has been measured by
an ideal voltmeter. Which of the following can be
calculated?

6
In an ideal differential amplifier shown in the figure, a large value of (R
E).

7
The effect of current shunt feedback in an amplifier is to
8
The input resistance R
i of the amplifier shown in the figure is

9
For an n-channel MOSFET and its transfer curve shown in the figure, the threshold voltage is


10
Given
$${r_d} = 20K\Omega ,\,\,{I_{DSS}}\, = \,10mA,\,\,{V_P} = - 8V$$

Transconductance in milli-Siemens (mS) and voltage gain of the amplifier are respectively.
11
Given
$${r_d} = 20K\Omega ,\,\,{I_{DSS}}\, = \,10mA,\,\,{V_P} = - 8V$$

Zi and Zo of the circuit are respectively
12
For an npn transistor connected as shown in the figure, V
BE = 0.7 volts. Given that reverse saturation current of the junction at room temperature $${300^0}$$ K is $${10^{ - 13}}\,{\rm A}$$, the emitter current is $$\left( {\eta \, = \,1} \right)$$

13
The circuit using a
BJT with β = 50 and V
BE = 0.7 V is shown in the figure. The base current I
B and collector voltage V
C are respectively

14
A symmetric three-level midtread quantizer is to be designed assuming equiprobable occurrence of all quantization levels.
If the input probability density function is divided into three regions as shown in figure, the value of 'a' in the figure is
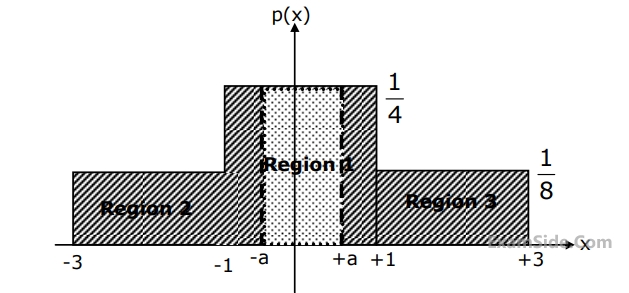
15
A symmetric three-level midtread quantizer is to be designed assuming equiprobable occurrence of all quantization levels.
The quantization noise power for the quantization region between –a and +a in the figure is
16
A signal as shown in figure is applied to a matched filter. Which of the following does represent the output of this matched filter?
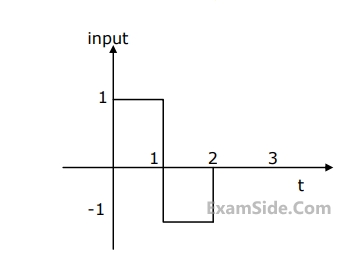
17
Noise with uniform power spectral density of N0 W/Hz is passed through a filter H(ω ) = 2exp (-jωtd) followed by an ideal low pass filter of bandwidth B Hz. The output noise power in Watts is
18
An output of a communication channel is a random variable 'V' with the probability density function as shown in the figure. The mean square value of 'V' is

19
A carrier is phase modulated (PM) with frequency deviation of 10 kHz by a single
tone frequency of 1 kHz. If the single tone frequency is increased to 2 kHz,
assuming that phase deviation remains unchanged, the bandwidth of the PM
signal is
20
A device with input x(t) and output y(t) is characterized by: y(t) = x2(t). An FM signal with frequency deviation of 90 kHz and modulating signal bandwidth of 5 kHz is applied to this device. The bandwidth of the output signal is
21
Which of the following analog modulation scheme requires the minimum
transmitted power and minimum channel bandwidth?
22
A unity feedback system is given as,$$$G\left(s\right)=\frac{K\left(1-s\right)}{s\left(s+3\right)}$$$ indicate the correct root locus diagram.
23
In the derivation of expression for peak percent overshoot,$$$M_p=exp\left(\frac{-\mathrm{πξ}}{\sqrt{1-\xi^2}}\right)\times100\%$$$ .Which one of the following conditions is NOT required?
24
A ramp input applied to an unity feedback system results in 5% steady state
error. The type number and zero frequency gain of the system are respectively.
25
Despite the presence of negative feedback, control systems still have problems of
instability because the
26
A linear system is equivalently represented by two sets of state equations. $$\mathop x\limits^ \bullet = \,\,{\rm A}X\,\, + BU$$ and $$\mathop W\limits^ \bullet = \,\,CW\,\, + DU.$$ The eigen values of the representations are also computed as $$\left[ \lambda \right]\,\,\,\,and\,\,\,\,\left[ \mu \right].$$ Which one of the following statements is true?
27
A double integrator plant, $$G(s) = {K \over {{s^2}}},H(s) = 1$$ is to be compensated to achieve the damping ratio $$\zeta = 0.5$$ and an undamped natural frequency, $${\omega _n} = 5$$ rad/sec. Which one of the following compensator $${G_c}(s)$$ will be suitable?
28
The open loop transfer function of a unity feedback system is given by
G(s)=$${{3{e^{ - 2s}}} \over {s\left( {s + 2} \right)}}.$$
The gain and phase crossover frequencies in rad/sec are, respectively
29
The polar diagram of a conditionally stable system for open loop gain K=1 is
shown in figure. The open loop transfer function of the system is known to be
stable. The closed loop system is stable for

30
The open loop transfer function of a unity feedback system is given by
g(s)=$${{3{e^{ - 2s}}} \over {s\left( {s + 2} \right)}}.$$
Based on the above results, the gain and phase margins of the system will be
31
Which one of the following polar diagrams corresponds to a lag network?
32
The transistors used in a portion of the TTL gate shown in figure have β=100. the base-emitter voltage of is 0.7V for a transistor in active region and 0.75V for a transistor in saturation . If the sink current I=1mA and the output is at logic 0,
then the current $${I_R}$$ I will be equal to

33
Both transistors T1 and T2 in figure have a threshold voltage of 1 Volt. The device parameters $${K_1}$$ and $${K_2}$$ of $${T_1}$$ and $${T_2}$$ are, respectively, 36 µA/ $${V^2}$$ and
and 9$$9\,A/{V^2}$$. The output voltage $${V_0}$$ IS

34
The present output Qn of an edge triggered JK flip-flop is logic 0. If J=1, then
Qn+1
35
Decimal 43 in Hexadecimal and BCD number system is respectively
36
The given figure shows a ripple counter using positive edge triggered flip-flops. If the
present state of counter is Q
2 Q
1 Q
0 = 011, then its next state ( Q
2 Q
1 Q
0 ) will be

37
The Boolean function f implemented in the figure using two input multiplexers is

38
The Boolean expression for the truth table shown is
| A |
B |
C |
D |
| 0 |
0 |
0 |
0 |
| 0 |
0 |
1 |
0 |
| 0 |
1 |
0 |
0 |
| 0 |
1 |
1 |
1 |
| 1 |
0 |
0 |
0 |
| 1 |
0 |
1 |
0 |
| 1 |
1 |
0 |
1 |
| 1 |
1 |
1 |
0 |
39
Many circles are drawn in a Smith chart used for transmission line calculations. The circles shown in Fig. represent

40
Two identical and parallel dipole antennas are kept apart by a distance $$\lambda /4$$ of in the H-plane. They are fed with equal currents but the right most antenna has a phase shift of +90°. The radiation pattern is given as
41
Which one of the following does represent the electric field lines for the $$T{E_{02}}$$ mode in the cross-section of a hollow rectangular metallic waveguide?
42
Refractive index of glass is 1.5. Find the wavelength of a beam of light with a frequency of $${10^{14}}$$ Hz in glass. Assume velocity of light is $$3\,\, \times \,{10^8}$$ m/s in vacuum.
43
Voltage standing wave pattern in a lossless transmission line with characteristic impedance 50 $$\Omega $$ and a resistive load is shown in Fig.

The reflection coefficient is given by
44
Voltage standing wave pattern in a lossless transmission line with characteristic impedance 50 $$\Omega $$ and a resistive load is shown in Fig.

The value of the load resistance is
45
Characteristic impedance of a transmission line is 50$$\Omega $$. Input impedance of the open-circuited line is $${Z_{oc}} = 100\, + \,j\,\,150\Omega .$$ When the transmission line is short-circuited the value of the input impedance will be
46
The magnetic field intensity vector of a plane wave is given by
$$\overline H \left( {x,y,z,t} \right) = 10\,\sin \left( {50000t + 0.004x + 30} \right){\mathop a\limits^ \cap _y}$$
Where $${\mathop a\limits^ \cap _y}$$ denotes the unit vector in $$y$$ direction. The wave is propagating with a phase velocity
47
A silicon sample 'A' is doped with 1018 atoms/cm3 of Boron. Another sample 'B' of
identical dimensions is doped with 1018 atoms/cm3 of Phosphorus. The ratio of
electron to hole mobility is 1/3. The ratio of conductivity of the sample A to B is
48
A Silicon PN junction diode under reverse bias has depletion region of width 10
µm. The relative permittivity of Silicon, ɛr = 11.7 and the permittivity of free space ɛ0 = 8.854 × 10-12 F/m.The depletion capacitance of the diode per square meter is
49
The Zener diode in the regulator circuit shown in figure has a Zener voltage of
5.8 Volts and a Zener knee current of 0.5 mA. The maximum load current drawn
from this circuit ensuring proper functioning over the input voltage range
between 20 and 30 Volts, is

50
A MOS capacitor made using p-type substrate is in the accumulation mode. The
dominant charge in the channel is due to the presence of
51
The band gap of Silicon at room temperature is:
52
A Silicon PN junction at a temperature of 20°C has a reverse saturation current of
10 pico-Amperes (pA). The reverse saturation current at 40°C for the same bias
is approximately
53
The primary reason for the widespread use of Silicon in semiconductor device
technology is
54
The Dirac delta Function $$\delta \left( t \right)$$ is defined as
55
In what range should $$Re(s)$$ remain so that the laplace transform of the function $${e^{\left( {a + 2} \right)t + 5}}$$ exists?
56
Match the following and choose the correct combination
Group $$-$$ $${\rm I}$$
$$E.$$ Newton $$-$$ Raphson method
$$F.$$ Runge-Kutta method
$$G.$$ Simpson's Rule
$$H.$$ Gauss elimination
Group $$-$$ $${\rm II}$$
$$(1)$$ Solving non-linear equations
$$(2)$$ Solving linear simultaneous equations
$$(3)$$ Solving ordinary differential equations
$$(4)$$ Numerical integration method
$$(5)$$ Interpolation
$$(6)$$ Calculation of eigen values
57
The following differential equation has $$3{{{d^2}y} \over {d{t^2}}} + 4{\left( {{{dy} \over {dt}}} \right)^3} + {y^2} + 2 = x$$
58
A solution of the differential equation $${{{d^2}y} \over {d{x^2}}} - 5{{dy} \over {dx}} + 6y = 0\,$$ is given by
59
A fair dice is rolled twice. The probability that an odd number will follow an even number is
60
$$\nabla \times \left( {\nabla \times P} \right)\,\,$$ where $$P$$ is a vector is equal to
61
The value of the integral $$1 = {1 \over {\sqrt {2\pi } }}\,\,\int\limits_0^\infty {{e^{ - {\raise0.5ex\hbox{$\scriptstyle {{x^2}}$}
\kern-0.1em/\kern-0.15em
\lower0.25ex\hbox{$\scriptstyle 8$}}}}} \,\,dx\,\,\,$$ is ________.
62
If $$A = \left[ {\matrix{
2 & { - 0.1} \cr
0 & 3 \cr
} } \right]$$ and $${A^{ - 1}} = \left[ {\matrix{
{{\raise0.5ex\hbox{$\scriptstyle 1$}
\kern-0.1em/\kern-0.15em
\lower0.25ex\hbox{$\scriptstyle 2$}}} & a \cr
0 & b \cr
} } \right]$$ then $$a+b=$$
63
Given an orthogonal matrix $$A = \left[ {\matrix{
1 & 1 & 1 & 1 \cr
1 & 1 & { - 1} & { - 1} \cr
1 & { - 1} & 0 & 0 \cr
0 & 0 & 1 & { - 1} \cr
} } \right]$$ then the value of $${\left( {A{A^T}} \right)^{ - 1}}$$ is
64
Given the matrix $$\left[ {\matrix{
{ - 4} & 2 \cr
4 & 3 \cr
} } \right],$$ the eigen vector is
65
Consider an 8085 microprocessor system
If in addition following code exists from 0109H onwards ORI 40H, ADD M What will be the result in the accumulator after the last instruction is executed
66
Consider an 8085 microprocessor system
The following program starts at locaton 0100H.
LXI SP, 00FF
LXI H, 0107
MVI A, 20H
SUB M
The contents of accumulator wnen the program counter reaches 0109H is
67
What memory address range is NOT represented by chip 1 and chip 2 in
figure? A
0 to A
15 in this figure are the address lines and CS means Chip Select.

68
The h parameters of the circuit shown in Fig. are
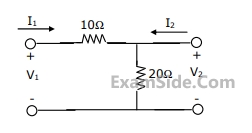
69
The ABCD parameters of an ideal n:1 transformer shown in Fig. are $$\left[ {\matrix{
n & 0 \cr
0 & X \cr
} } \right]$$. The value of X will be

70
For the circuit in figure, the phase current $${{\rm I}_1}$$ is
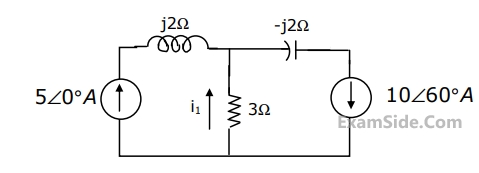
71
In a series $$RLC$$ circuit $$R = 2\,k\Omega ,\,\,\,L = \,1H$$ and $$C = \,1/400\,\mu F.$$ The resonant frequency is
72
If R1 = R2 = R4 = R and R3 = 1.1R in the bridge circuit shown in figure, then the reading in the ideal voltmeter connected between a
and b is

73
A square pulse of 3 volts amplitude is applied to C-R circuit shown in figure. The
capacitor is initially uncharged. The output voltage v0 at time t=2 sec is
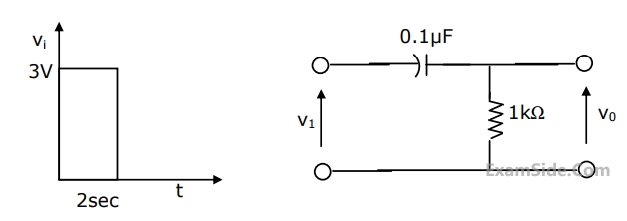
74
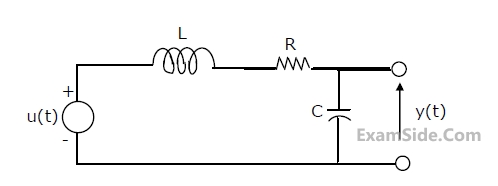
The condition on R, L and C such that the step response y(t) in figure has no
oscillations, is
75
For the circuit shown in figure, Thevenin’s voltage and Thevenin’s equivalent
resistance at terminals a – b is

76
The maximum power that can be transferred to the load resistor R
L from the voltage source in figure is

77
Impedance Z as shown in the figure is:

78
The output y(t) of a linear time invariant system is related to its input x(t) by the following equation: y(t) = 0.5 x $$(t - {t_d} + T) + \,x\,(t - {t_d}) + 0.5\,x(t - {t_d} - T)$$. The filter transfer function $$H(\omega )$$ of such a system is given by
79
Match the following and choose the correct combination.
GROUP 1
E- continuous and aperiodic signal
F- continuous and periodic signal
G- discrete and aperiodic signal
H- discrete and periodic signal
Group 2
1- Fourier representation is continuous and aperiodic
2- Fourier representation is discrete and aperiodic
3- Fourier representation is continuous and periodic
4- Fourier representation is discrete and periodic
80
The value of the integral $$\,I = {1 \over {\sqrt {2\,\,\pi } }}\int\limits_0^\infty {\exp \left( { - {{{x^2}} \over 8}} \right)dx} $$ is
81
The derivative of the symmetric function drawn in Fig .1 will look like

82
The function x(t) is shown in Fig. Even and odd parts of a unit-step function u(t) are respectively.

83
A signal x(n)$$ = \sin ({\omega _0}\,n + \phi )$$ is the input to a linear time-invariant system having a frequency response $$H({e^{j\omega }})$$.If the output of the system is $$Ax(n - {n_0})$$, then the most general form of $$\angle H({e^{j\omega }})$$ will be
84
For a signal x(t) the Fourier transform is X(f). Then the inverse Fourier transform of X(3f+2) is given by
85
Which of the following can be impulse response of a causal system?
86
The region of convergence of z-transform of the sequence $${\left( {{5 \over 6}} \right)^n}u(n) - {\left( {{6 \over 5}} \right)^n}u( - n - 1)$$ must be
87
A sequence x(n) has non-zero values as shown in figure. 1

The Fourier transform of y(2n) will be
88
A sequence x(n) has non-zero values as shown in Fig.

The sequence
$$$y(n)=\left\{\begin{array}{l}x\left(\frac n2-1\right)\;\;\;for\;n\;even\\0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;for\;n\;odd\end{array}\right.$$$
will be
89
In what range should Re(s) remain so that the Laplace transform of the function e(a+2)t+5 exists?
90
Let x(n) = $${\left( {{1 \over 2}} \right)^n}$$ u(n), y(n) = $${x^2}$$, and Y ($$({e^{j\omega }})\,$$ be the Fourier transform of y(n). Then Y ($$({e^{jo}})$$ is
91
Choose the function f (t );−$$\infty$$ < 1 < +$$\infty$$, for which a Fourier series cannot be
defined.





















 The reflection coefficient is given by
The reflection coefficient is given by  The value of the load resistance is
The value of the load resistance is 













