1
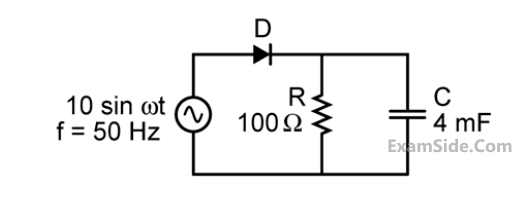
The figure shows a half-wave rectifier. The diode D is ideal. The average steady-state current
(in Amperes) through the diode is approximately ____________.
2
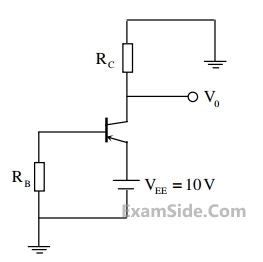
In the circuit shown, the PNP transistor has $$\left|{\mathrm V}_\mathrm{BE}\right|=0.7\;\mathrm V$$ and β = 50. Assume that R
B = 100 kΩ.
For V
0 to be 5 V, the value of R
C ( in kΩ) is _____________.
3
In the circuit shown, the silicon BJT has $$\beta \,\,\,\,50.\,\,\,\,\,$$ Assume $${V_{BE}}\,\,\, = \,\,\,0.7$$ and $${V_{CE\left( {sat} \right)}}\, = \,0.2V.$$ Which one of the following statements is correct ?

4
The desirable characteristics of a transconductance amplifier are
5
Assuming that the Op-amp in the circuit shown is ideal, V
0 is given by

6
Let $$X(t)$$ be a wide sense stationary $$(WSS)$$ random procfess with power spectral density $${S_x}\left( f \right)$$. If $$Y(t)$$ is the process defined as $$Y(t) = X(2t - 1)$$, the power spectral density $${S_y}\left( f \right)$$ is
.
7
A real band-limited random process $$X( t )$$ has two -sided power spectral density
$$${S_x}\left( f \right) = \left\{ {\matrix{
{{{10}^{ - 6}}\left( {3000 - \left| f \right|} \right)Watts/Hz} & {for\left| f \right| \le 3kHz} \cr
0 & {otherwise} \cr
} } \right.$$$
Where f is the frequency expressed in $$Hz$$. The signal $$X( t )$$ modulates a carrier cos $$16000$$ $$\pi t$$ and the resultant signal is passed through an ideal band-pass filter of unity gain with centre frequency of $$8kHz$$ and band-width of $$2kHz$$. The output power (in Watts) is ______.
8
Let $${X_1},\,{X_2},$$ and $${X_3}$$ be independent and identically distributed random variables with the uniform distribution on $$\left[ {0,\,1} \right]$$. The probability $$P\left\{ {{X_1} + {X_2} \le {X_3}} \right\}$$ is ___________ .
9
In a PCA system, the signal $$m(t) = \{ \sin (100\,\pi \,t)\, + \cos (100\,\pi \,t\} $$ V is sampled at the Nyquist rate. The samples are processed by a uniform quantizer with step size 0.75 V. The minimum data rate of the PCM system in bits per second is________________
10
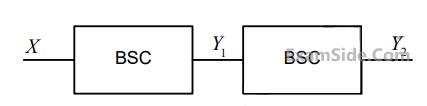
A binary random variable X takes the value of 1 with probability 1/3. X is input to a casade of 2 independent identical binary symmetric channels (BSCs) each with crossover probability 1/2. The output of BSCs are the random variables $${Y_1}$$ and $${Y_2}$$ as shown in the figure.
11
Consider an FM signal $$f\left(t\right)\;=\;\cos\left[2{\mathrm{πf}}_\mathrm c\mathrm t\;+\;{\mathrm\beta}_1\sin\;2{\mathrm{πf}}_1\mathrm t\;+\;{\mathrm\beta}_2\sin\;2{\mathrm{πf}}_2\mathrm t\right]$$ . The maximum
deviation of the instantaneous frequency from the carrier frequency fc
is
12
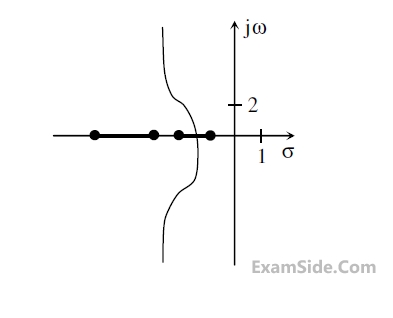
In the root locus plot shown in the figure, the pole/zero marks and the arrows have been
removed. Which one of the following transfer functions has this root locus?
13
The steady state error of the system shown in the figure for a unit step input is _______.
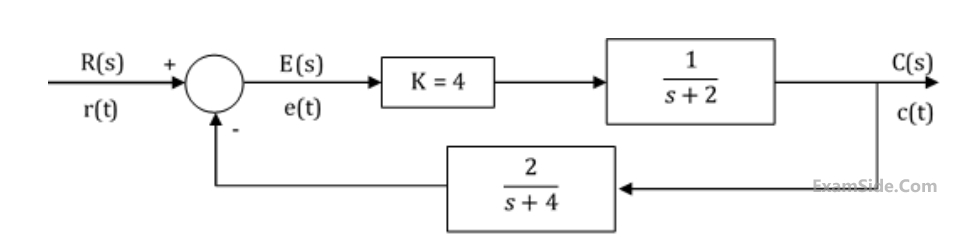
14
Consider the following block diagram in the figure.
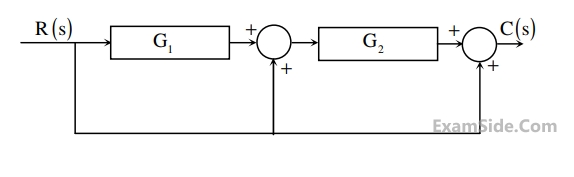
The transfer function $$\frac{\mathrm C\left(\mathrm s\right)}{\mathrm R\left(\mathrm s\right)}$$ is
15
The input $$-3\mathrm e^{2\mathrm t}\;\mathrm u\left(\mathrm t\right)$$, where u(t) is the unit step function, is applied to a system with transfer
function $$\frac{s-2}{s+3}$$. If the initial value of the output is -2, then the value of the output at steady
state is __________.
16
The state equation of a second-order linear system is given by $$\mathop x\limits^ \bullet \left( t \right) = Ax\left( t \right),x\left( 0 \right) = {x_0}.$$
For $${x_0} = \left[ {\matrix{
1 \cr
{ - 1} \cr
} } \right],x\left( t \right) = \left[ {\matrix{
{{e^{ - t}}} \cr
{ - {e^{ - t}}} \cr
} } \right]$$ and for $${x_0} = \left[ {\matrix{
0 \cr
1 \cr
} } \right],x\left( t \right) = \left[ {\matrix{
{{e^{ - t}}} & { - {e^{ - 2t}}} \cr
{ - {e^{ - t}}} & { + 2{e^{ - 2t}}} \cr
} } \right]$$ when $${x_0} = \left[ {\matrix{
3 \cr
5 \cr
} } \right],x\left( t \right)$$ is
17
If WL is the Word Line and BL the Bit Line, an SRAM cell is shown in
18
In the circuit shown, 𝑊𝑊 and 𝑌𝑌 are MSBs of the control inputs. The output 𝐹𝐹 is given by

19
If X and Y are inputs and the Difference (D = X – Y) and the Borrow (B) are the outputs, which one of the following diagrams
implements a half-subtractor?
20
The circuit shown in the figure is a

21
Consider the multiplexer based logic circuit shown in the figure.

Which one of the following Boolean functions is realized by the circuit?
22
In the following figure, the transmitter Tx sends a wideband modulated RF signal via a coaxial cable to the receiver Rx. The output impedance $${Z_T}$$ of Tx, the characteristic impedance $${Z_0}$$ of the cable and the input impedance $${Z_R}$$ of Rx are all real.
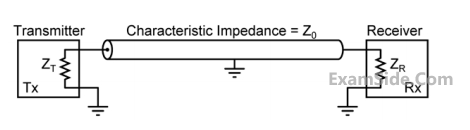
Which one of the following statements is TRUE about the distortion of the received signal due to impedance mismatch?
23
A region shown below contains a perfect conducting half-space and air. The surface current $${\overrightarrow K _{_s}}$$ on the surface of the perfect conductor is $${\overrightarrow K _{_s}} = \widehat x\,2$$ amperes per meter. The tangential $$\overrightarrow H $$ field in the air just above the perfect conductor is
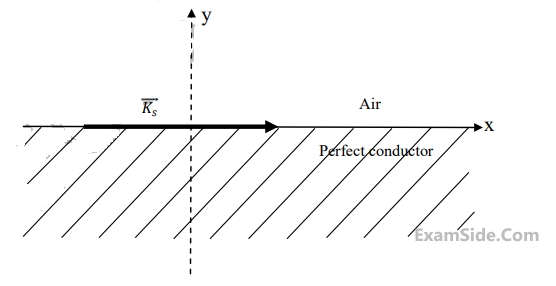
24
Assume that a plane wave in air with an electric field
$$\overrightarrow E = 10\cos \left( {\omega t - 3x - \sqrt {3z} } \right){\widehat a_{_y}}\,\,\,V/m$$ is incident
on a non-magnetic dielectric slab of relative permittivity $$3$$ which covers the region $$z > 0$$ . The angle of transmission in the dielectric slab is _______ degrees.
25
Consider an air filled rectangular waveguide with a cross-section of $$5\,\,cm\,\, \times \,\,3\,cm$$. For this waveguide, the cut-off frequency (in MHz) of $$T{E_{21}}\,$$ mode is __________________
26
Given the vector $$$\mathrm A=\left(\cos\;\mathrm x\right)\left(\sin\;\mathrm y\right)\;{\widehat{\mathrm a}}_\mathrm x\;+\;\left(\sin\;\mathrm x\right)\left(\cos\;\mathrm y\right){\widehat{\mathrm a}}_\mathrm y$$$ where $${\widehat{\mathrm a}}_\mathrm x$$ , $${\widehat{\mathrm a}}_\mathrm y$$ denote unit vectors
along x, y directions, respectively. The magnitude of curl of A is ________
27
A thin P-type silicon sample is uniformly illuminated with light which generates excess
carriers. The recombination rate is directly proportional to
28
At T = 300 K, the hole mobility of a semiconductor $$\mu_p\;=500\;cm^2/V-s$$ and $$\frac{kT}q\;=\;26\;mV$$.The hole diffusion constant Dp in cm2/s is__________.
29
In MOSFET fabrication, the channel length is defined during the process of
30
An ideal MOS capacitor has boron doping concentration of 1015 cm-3 in the substrate. When a gate voltage is applied, a depletion region of width 0.5 $$\mu m$$ is formed with a surface (channel) potential of 0.2V. Given that $${\varepsilon _0} = 80854 \times {10^{ - 14}}F/cm$$ and the relative permittivities of silicon and silicon dioxide are 12 and 4, respectively, the peak electric field (in V/ $$\mu m$$ ) in the oxide region is ______
31
The slope of the ID vs. VGS curve of an n-channel MOSFET in linear region is 10-3$${\Omega ^{ - 1}}$$ at VDS = 0.1V. For the same device, neglecting channel length modulation, the slope of the $$\sqrt {{{\rm I}_D}} $$ vs. V GS curve (in $$\sqrt A /V$$ ) under saturation region is approximately ______.
32
For the MOSFET M
1 shown in the figure, assume W/L =2, V
DD = 2.0 V, $$\mu n$$ C
OX = 100$$\mu {\rm A}/{V^2}$$ and V
TH =0.5 V. The transistor M
1 switches from saturation region to linear regionm when V
in(in Volts) is _____

33
Which one of the following statements is NOT true for a square matrix $$A$$?
34
The maximum value of the function $$\,f\left( x \right) = \ln \left( {1 + x} \right) - x$$ (where $$x > - 1$$ ) occurs at $$x=$$________.
35
The maximum value of $$f\left( x \right) = 2{x^3} - 9{x^2} + 12x - 3$$
in the interval $$\,0 \le x \le 3$$ is __________.
36
If $$z=xy$$ $$ln(xy),$$ then
37
An unbiased coin is tossed an infinite number of times. The probability that the fourth head appears at the tenth toss is
38
A fair coin is tossed repeatedly till both head and tail appear at least once. The average number of tosses required is ________.
39
Let $${X_1},{X_{2,}}$$ and $${X_{3,}}$$ be independent and identically distributed random variables with the uniform distribution on $$\left[ {0,1} \right].$$ The probability $$P\left\{ {{X_1} + {X_2} \le {X_3}} \right\}$$ is _______.
40
Which ONE of the following is a linear non - homogeneous differential equation , where $$x$$ and $$y$$ are the independent and dependent variables respectively?
41
Match the application to appropriate numerical method
Applications
$$P1:$$ Numerical integration
$$P2:$$ Solution to a transcendental equation
$$P3:$$ Solution to a system of linear equations
$$P4:$$ Solution to a differential equation
Numerical Method
$$M1:$$ Newton-Raphson Method
$$M2:$$ Runge-Kutta Method
$$M3:$$ Simpson's $$1/3-$$rule
$$M4:$$ Gauss Elimination Method
42
Consider the building block called 'Network N' shown in the figure.
Let $$C = 100\,\mu F\,\,$$ and $$R = 10\,k\Omega $$.
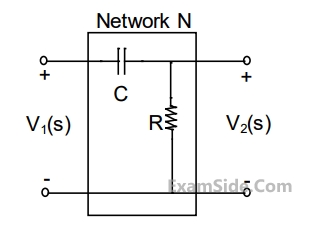
Two such blocks are connected in cascade, as shown in the figure.
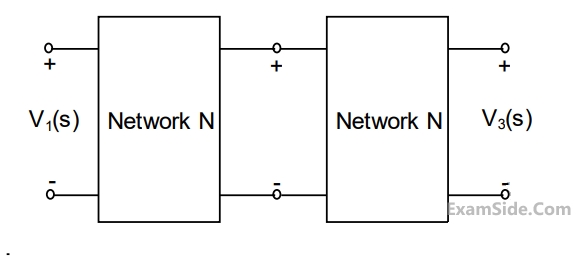
The transfer function $${{{V_3}\left( s \right)} \over {{V_1}\left( s \right)}}$$ of the cascaded network is
43
For the Y-network shown in the figure, the value of R1 (in Ω) in the equivalent ∆ -network is ________.

44
In the circuit shown in the figure, the value of node voltage V
2 is

45
In the circuit shown in the figure, the angular frequency $$\omega$$ (in rad/s), at which the Norton equivalent impedance as seen from terminals b-b' is purely resistive, is _______.
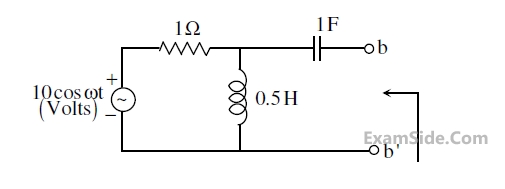
46
A series RC circuit is connected to a DC voltage source at time t = 0. The relation between the source voltage VS, the resistance R, the capacitance C, and the current i(t) is given below:
$$$V_{s\;}=\;Ri(t)+\frac1c\int_0^ti(u)du$$$
Which one of the following represents the current f(t)?
47
In the figure shown, the value of the current I (in Amperes) is __________.
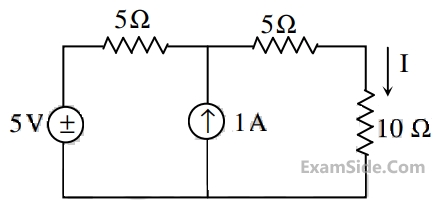
48
The input $$ - 3{e^{2t}}\,\,u\left( t \right)$$, where u(t) is the unit step function$$\, {{s - 2} \over {s + 3}}$$. If the initial value of the output is -2, then the value of the output at steady state is _____.
49
Let h(t) denote the impulse response of a casual system with transfer function $${1 \over {s + 1}}$$. Consider the following three statements.
S1: The system is stable.
S2: $${{h\left( {t + 1} \right)} \over {h\left( t \right)}}$$ is independent of t for t > 0.
S3: A non-casual system with the same transfer function is stable.
For the above system,
50
For an all-pass system H(z)= $${{({z^{ - 1}} - b)} \over {(1 - a{z^{ - 1}})}}$$ where $$\left| {H({e^{ - j\omega }})} \right| = \,1$$ , for all $$\omega $$. If Re (a) $$ \ne $$ 0,$${\mathop{\rm Im}\nolimits} (a) \ne 0$$ then b equals
51
The z-transform of the sequence x$$\left[ n \right]$$ is given by x(z)= $${1 \over {{{(1 - 2{z^{ - 1}})}^2}}}$$ , with the region of convergence $$\left| z \right| > 2$$. Then, $$x\left[ 2 \right]$$ is ____________________.
52
Let $${H_1}(z) = {(1 - p{z^{ - 1}})^{ - 1}},{H_2}(z) = {(1 - q{z^{^{ - 1}}})^{ - 1}}$$ , H(z) =$${H_1}(z)$$ +r $${H_2}$$. The quantities p, q, r are real numbers. Consider , p=$${1 \over 2}$$, q=-$${1 \over 4}$$ $$\left| r \right|$$ <1. If the zero H(z) lies on the unit circle, the r = ____________________________.
53
A modulated signal is $$y\left( t \right)\, = \,\,\,\,\,\,\,\,\,m\left( t \right)\,\cos \left( {40000\pi t} \right),$$ where the baseband signal $$m\left( t \right)\,$$ has frequency components less than 5 kHz only. The minimum required rate (in kHz) at which $$y\,\,\left( t \right)$$ should be sampled to recover $$m\,\,\left( t \right)$$ is ________.
54
Let $$\,x\,\,\left( t \right)\,\,\, = \,\,\,\cos \,\,\,\left( {10\pi t} \right)\,\, + \,\,\cos \,\,\left( {30\pi t} \right)$$ be sampled at $$20\,\,\,Hz$$ and reconstructed using an ideal low-pass filter with cut-off frequency of $$20\,\,\,Hz$$. The frequency/frequencies present in the reconstructed signal is/are.
55
The phase response of a passband waveform at receiver is given by $$\varphi \,(f) = - 2\,\pi \,\alpha \,(f - {f_c}) - \,2\pi \beta \,{f_c}$$
where $${f_c}$$ is the centre frequency, and $$\alpha $$ and $$\beta $$ are positive constants. The actual signal propagation delay from the trasmitter to receiver is







 The transfer function $$\frac{\mathrm C\left(\mathrm s\right)}{\mathrm R\left(\mathrm s\right)}$$ is
The transfer function $$\frac{\mathrm C\left(\mathrm s\right)}{\mathrm R\left(\mathrm s\right)}$$ is


 Which one of the following statements is TRUE about the distortion of the received signal due to impedance mismatch?
Which one of the following statements is TRUE about the distortion of the received signal due to impedance mismatch?






