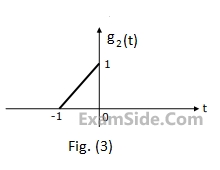Assume that the OP_AMP in the figure, ideal

(a) Obtain an expression for V₀ in terms of V_s, R, and the reverse saturation current I_s of the transiostor.

(b) If R = 1$$\Omega $$, I_s = 1pA and the thermal voltage V_T = 25mV, then what is the value of the output voltage V₀ for an input voltage V_s = 1V?

(c) Suppose that the transistor in the feedback path is replaced by a p-n junction diode with a reverse saturation current of I_s. The p-side of the diode is connected to node A and the n-side to node B. Then what is the expression for V₀ in terms V_s, R and I_s ?

The current gain of a BJT is

An emitter-follower amplifier is shown in the figure, Z_i is the impedance looking into the base of the transistor and Z₀ is the impedance looking into the emitter of the transistor

(a)Draw the small signal equivalent circuit of the amplifier.
(b)Obtain an expression for z_i.
(c)Obtain an expression for z₀.

An npn BJT has g_m = 38 mA/V, $${C_\mu }\, = {10^{ - 14}}$$ F, $${C_\pi }\, = 4\, \times {10^{ - 13}}\,F$$ and DC current gain $$\beta \, = \,90$$. For this transistor f_T and $${f_\beta }$$ are

The Oscillator circuit shown in the figure is

The ideal Op-Amp has the following characteristics.

Consider the following two statements.

Statement 1: Astable Multivibrator can be used for generating Square Wave.

Statement 2: Bistable Multivibrator can be used for storing binary information.

The Inverting Op-Amp shown in the figure, has an Open-loop gain of 100. The closed loop gain $${{{V_o}} \over {{V_s}}}$$ is

In the figure assume the Op-Amps to be ideal. The output V₀ of the circuit is

An Amplifier using an Op-Amp with a Slew-Rate SR = V/$$\mu $$sec, has a gain of 40 dB. If this amplifier has to faith fully amplify sinsoidal signals from dc to 20 KHz. Without introducing any Slew Rate induced distortion, then the input signal level must not exceed.

The PDF of a Gaussian random variable X is given by $${p_x}(x) = \,{1 \over {3\sqrt {2\pi } }}\,\exp \,[ - \,{(x - 4)^2}/18]$$.

The probability of the event {X = 4} is

A band limited signal is sampled at the Nyquist rate. The signal can be recovered by passing the samples through

During transmission over a communication channel, bit errors occur independently with probability 'p'. If a block of n bits is transmitted, the probability of at most one bit error is equal to

A video transmission system transmits 625 picture frames per second. Each frame consists of a $$400\,\, \times \,\,400$$ pixel grid with 64 intensity levels per pixel. The data rate of the system is

The root-locus diagram for a closed loop feedback system is shown in Figure. The system is overdamped.

A feedback control system is shown in figure (a) Draw the signal-flow graph that represents the system.
(b) Find the total number of loops in the graph and determine the loop-gains of all the loops.
(c) Find the number of all possible combination of non-touching loops taken two at a time.
(d) Determine the transfer function of the system using the signal-flow graph.

If the characteristic equation of a closed-loop system is s² + 2s + 2 =0, then the system is

The equivalent of the block diagram in Figure is given as

An electrical system and its signal-flow graph representations are shown in Figure (a) and (b) respectively. The values of G₂ and H, respectively are

The feedback control system in Figure is stable

Consider the feedback control system shown in figure.
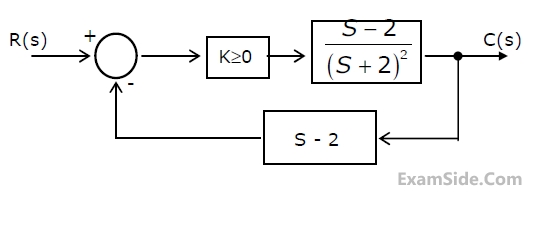
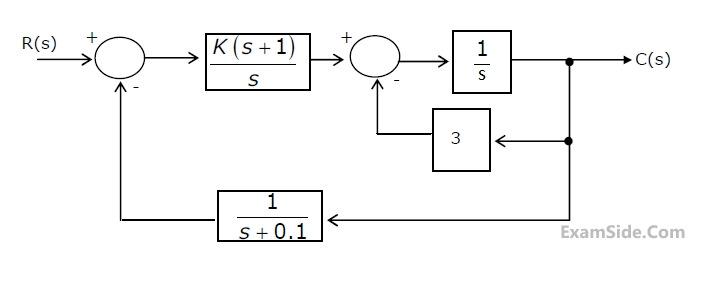
(a) Find the transfer function of the system and its characteristic equation.

(b) Use the Routh-Hurwitz criterion to determine the range of 'K' for which the system is stable.

Given the $$G\left(s\right)H\left(s\right)=\frac K{s\left(s+1\right)\left(s+3\right)}$$, the point of intersection of the asymptotes of the root loci with the real axis is

The Nyquist plot for the open-loop transfer function G(s) of a unity negative feedback system is shown in figure. if G(s) has no pole in the right half of s-plane, the number of roots of the system characteristic equation in the right half of s-plane is

The open-loop DC gain of a unity negative feedback system with closed-loop transfer function $${{s + 4} \over {{s^2} + 7s + 13}}$$ is

For the feedback control system shown in the figure, the process transfer function is G_p(s) = $${1 \over {s(s + 1)}},$$ and the amplification factor of the Power amplifier is K$$ \ge $$0. The design specifications required for the system, time constant is 1 sec and a damping ratio of 0.707.
(a) Find the desired location of the closed loop poles.
(b) Write down the requiredcharacteristic equation for the system. Hense determine the PD controller transfer function G_p(s) when K = 1.
(c) Sketch the root-locus for the system.

In the figure the LED

For the digital block shown in Figure. 2(a), the output Y=f(S₃,S₂,S₁,S₀) where S₃ is MSB and S₀ is LSB. Y is given in terms of minterms as $$Y\, = \,\sum m\left( {1,5,6,7,11,12,13,15} \right)$$ and its complements $$\overline Y \, = \,\sum m\left( {0,2,3,4,8,9,10,14} \right)$$.

(a) Enter the logical values in the given Karnaugh map [figure2(b)] for the output Y.
(b) Write down the expression for Y in sum-of products from using minimum number of terms.
(c) Draw the circuit for the digital logic boxes using four 2-input NAND gates only for each of the boxes.

The digital block in the figure is realized using two positive edge triggered D flip-flops. Assume that for t < t₀, Q₁ = Q₂ =0. The circuit in the digital block is given by

The 2’s complement representation of –17 is

For the ring oscillator shown in the figure, the propagation delay of each inverter is 100 pico sec. What is the fundamental frequency of the oscillator output?

In the TTL circuit in Figure 2.11, $${S_0}$$ to $${S_0}$$ are select lines and $${X_7}$$ and $${X_0}$$are input lines. $${S_0}$$ and $${X_0}$$ are LSB'. The output Y is

A transmission line is distortionless if

If a plane electromagnetic wave satisfies the equation $${{{\partial ^2}\,{E_x}} \over {\partial \,{z^2}}} = \,{c^2}{{{\partial ^2}\,{E_x}} \over {\partial \,{t^2}}},$$ the wave propagates in the

A uniform plane electromagnetic wave incident normally on a plane surface of a dielectric material is reflected with a VSWR of 3. What is the percentage of incident power that is reflected?

The phase velocity of waves propagating in a hollow metal waveguide is

The dominant mode in a rectangular waveguide is $$T{E_{10}}$$, because this mode has

A medium has breakdown strength of $$16$$ KV/m r.m.s. Its relative permeability is $$1.0$$ and relative permittivity is $$4.0$$. A plane electromagnetic wave is transmitted through the medium. Calculate the maximum possible power flow density and the associated magnetic filed.

In a uniform linear array, four isotropic radiating elements are spaced $$\lambda /4$$ apart. The progressive phase shift between the elements required for forming the main beam at 60° off the end-fire is

A medium wave radio transmitter operating at a wavelength of 492 m has a tower antenna of height 124m. What is the radiation resistance of the antenna?

A rectangular hollow metal waveguide has dimensions a = 2.29 cm and b = 1.02 cm. Microwave power at 10 GHz is transmitted through the waveguide in the $$T{E_{10}}$$ mode.
(a) Calculate the cut-off wavelength and the guide wavelength for this mode.
(b) What are the other (TE or TM) modes that can propagate through the waveguide?
(c) If a = b = 2.29 cm, what are the modes which can propagate through the waveguide?

A material has conductivity of 10^-2 mho/m and a relative permittivity of 4. The frequency at which the conduction current in the medium is equal to the displacement current is

MOSFET can be used as a

Solve the differential equation $${{{d^2}y} \over {d{x^2}}} + y = x\,\,$$ with the following conditions $$(i)$$ at $$x=0, y=1$$ $$(ii)$$ at $$x=0, $$ $${y^1} = 1$$

An 8085 microprocessor based system uses a 4K × 8-bit RAM whose starting address is AA00H. The address of the last byte in this RAM is

The circuit shown in Fig. is operating in steady-state with switch $${S_1}$$ closed. The switch $${S_1}$$ is opened at $$t\, = \,0$$.

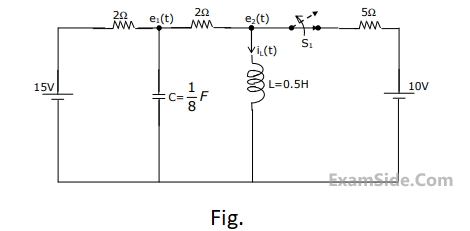
(a) Find $${i_L}\left( {{0^ + }} \right)$$.
(b) Find $${e_1}\left( {{0^ + }} \right)$$.
(c) Using nodal equations and Laplace transform approach, find an expression for the voltage across the capacitor for all $$t\, = \,0$$.

When the angular frequency $$\omega $$ in Fig. is varied from $$0$$ to $$\infty $$ the locus of the current phasor $${{\rm I}_2}$$ is given by

If each branch of a Delta circuit has impedance $$\sqrt 3 \,Z$$, then each branch of the equivalent Wye circuit has impedance

The Z parameters $${Z_{11}}$$ and $${Z_{21}}$$ for the 2-port network in Fig. are

The admittance parameters of a 2-port network shown in Fig. are given by $${Y_{11}} = \,2\,\,mho$$, $${Y_{12}}$$ = - 0.5 mho, $${Y_{21}}$$ = 4.8 mho, $${Y_{22}}$$ = 1 mho. The output port is terminated with a load admittance $${Y_L}$$ = 0.2 mho. Find $${E_2}$$ for each of the following conditions:

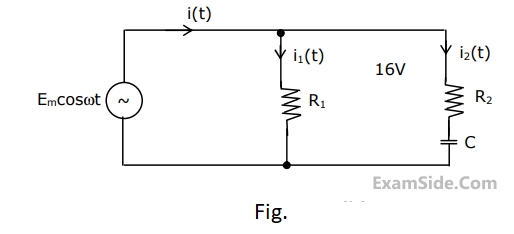
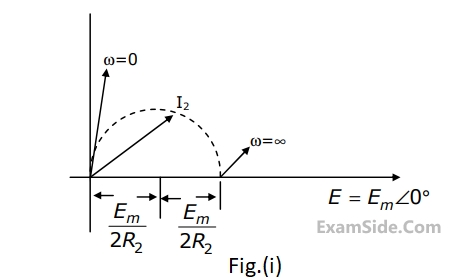
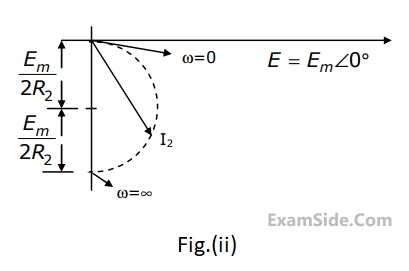
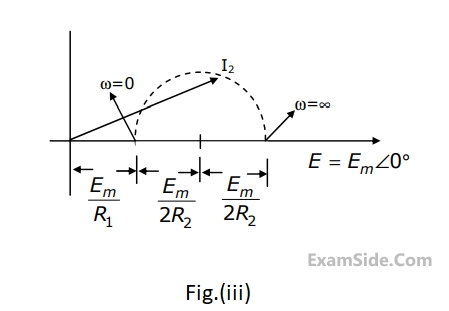
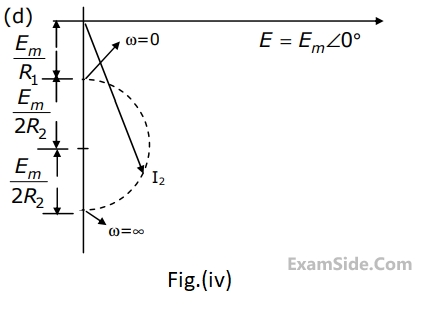
(a) $${E_1} = \,10\,\angle \,{0^{ \circ \,}}\,V$$
(b) $${I_1} = \,10\,\angle \,{0^{ \circ \,}}\,A$$
(c) A source $$10\,\angle \,{0^{ \circ \,}}\,V$$ in series with a 0.25 $$\Omega $$ resistor is connected to the input port.

The voltage e₀ in figure is

In figure, the value of the load resistor R which maximizes the power delivered to it is

For the circuit shown in the figure, determine the phasors E₂, E₀, I and I₁.

The admittance parameter Y₁₂ in the 2-port network in Figure is

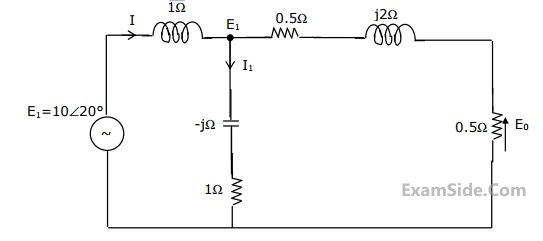
The voltage e₀ in Fig. is

If a signal f(t) has energy E, the energy of the signal f(2t) is equal to

The region of convergence of the z- transform of a unit step function is

The transfer function of a system is given by $$H\left( s \right) = {1 \over {{s^2}\left( {s - 2} \right)}}$$. The impulse response of the system is

The impulse response function of four linear system S1, S2, S3, S4 are given respectively by

$${h_1}$$(t), = 1;

$${h_2}$$(t), = U(t);

$${h_3}(t)\, = \,{{U(t)} \over {t + 1}}$$;

$${h_4}(t)\, = {e^{ - 3t}}U(t)$$ ,

where U (t) is the unit step function. Which of these system is time invariant, causal, and stable?

The Fourier transform $$G(\omega )$$ of the signal g(t) in Fig.(1) is given as
$$G(\omega ) = {1 \over {{\omega ^2}}}({e^{j\omega }} - j\omega {e^{j\omega }} - 1)$$.

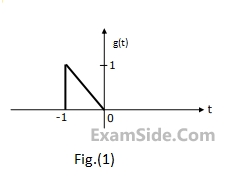
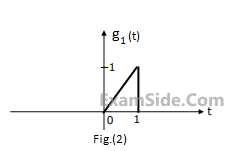
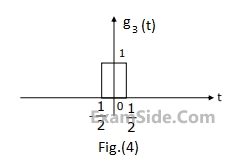
Using this information, and the time-shifting and time-scaling properties, determine and Fourier transform of signals in Fig (2), (3) and (4).

A band limited signal is sampled at the Nyquist rate. The signal can be recovered by passing the samples through

A base band signal g(t) band limited to 100 Hz modulates a carrier of frequency $${{f_0}}$$ Hz. The modulated signal g(t) $$\cos 2\,\pi \,{f_0}t$$ is transmitted over a channel whose input x and output y are related by $$y = 2x + {x^2}$$. The spectrum of g(t) is shown in Fig. Sketch the spectrum of the transmitted signal and the spectrum of the received signal.

The Nyquist sampling interval, for the signal Sinc(700t) + Sinc(500t) is

Let $$\delta (t)$$ denote the delta function. The value of the the integral $$\int\limits_{ - \infty }^\infty {\delta (t)} \,\,\cos \left( {{{3\,\,t} \over 2}} \right)dt$$ is

The PSD and the power of a signal g(t) are, respectively, S_g($$\omega$$) and P_g. The PSD and the power of the signal ag(t) are, respectively