GATE ECE 1995
GATE ECE
1
Shown that the system in Fig. is a double integrator. In other words, prove that the transfer gain is given by $${{{V_0}\left( s \right)} \over {{V_i}\left( s \right)}} = {1 \over {{{\left( {CRs} \right)}^2}}},$$ assume ideal OP -AMP
2
A transistor having $$\alpha$$ = 0.99 and VBE = 0.7 V, is used in the circuit of the figure.What is the value of the collector current?
3
A BJT is said to be operating in the saturation region if
4
An n-channel JFET has IDSS = 1 mA and Vp = -5 V. Its maximum transconductance is ______
5
A power Amplifier delivers 50 W output at 50% efficiency. The ambient temperature is 25$$^\circ $$ C. if the maximum allowable junction temperature is 150 $$^\circ $$ C, then the maximum thermal resistance $${\theta _{Jc}}$$ that can be tolerated is
6
The circuit shown, the figure supplies power to on 8 v speaker or L.S. The vaLUES OF $${I_C}$$ and $${V_{CE}}$$ for this ciruit will be
7
To obtain very high input and output impedances in a feedback Amplifier, the mostly used is
8
An op-Amp is used as a zero-crossing detector. If maximum output available from the Op-Amp is $$ \pm 12\,\,{V_{p - p}}$$ and the slew rate of the Op-Amp is 12 $$V/\mu $$ sec then the maximum frequency of the input signal that can be applied without causing a reduction in the P-P output is _____
9
A change in the value of the Emitter resistance (Re in a difference Amplifier.
10
In the given circuit if the voltage inputs V- and V+ are to be Amplified by the same Amplification factor, the value of 'R' should be
11
In the JFET circuit shown in Fig assume that R1||R2 = 1 M$$\Omega $$ and the total stray capacitance at the output to be 20 pF. The JFET used has gm = 2mA/V, Cgs = 20 pF and Cgd = 2 pF. Determine the upper cut-off frequency of the amplifier.
12
An RC-Coupled Amplifier is assumed to have a single-pole low frequency transfer function. The maximum lower-cutoff frequency allowed for the Amplifier to pass 50 Hz square wave with no more than 10% tilt is ______.
13
An Amplifier has an open-loop gain of 100 and its lower and upper-cut-off frequency of 100 Hz and 100 kHz respectively, a feedback network with a feedback factor of 0.99 is connected to the amplifier. the lower-and upper-cut-off frequency's are at ............and ............
14
If the number of bits per sample in a PCM system is increased from n to n+1, the improvement in signal-to-quantization noise ratio will be
15
The signal to quantization noise ratio in an n-bit PCM system
16
For a narrow band noise with Gaussian quadrature and inphase components, the probability density function of its enveolope will be
17
The step error coefficient of a system G(s)=$$\frac1{\left(s+6\right)\left(s+1\right)}$$ with unity feedback is
18
If $$L\left(f\left(t\right)\right)=\frac{2\left(s+1\right)}{s^2+2s+5}$$ then f(0+) and f($$\infty$$) are given by
[Note: 'L' stands for 'Laplace Transform of']
19
The final value theorem is used to find the
20
For a second order system, damping ratio $$\left(\xi\right)$$ , is 0 < $$\xi$$ < 1 ,then the roots of the characteristic polynomial are
21
Signal flow graph is used to find
22
The transfer function of a linear system is the
23
Non - minimum phase transfer function is defined as the transfer function
24
The minimum number of MOS transistors required to make a dynamic RAM cell is
25
An R-S latch is
26
A switch-tail ring counter is made by using a single D flip-flop. The resulting circuit is a
27
The output of the circuit shown in figure is equal to
28
A ROM is to be used to implement the Boolean functions given below:
$${F_1}$$$$(A,\,B,\,C,\,D) = ABCD + \bar A\,\overline B \,\bar C\,\bar D$$
$${F_2}(A,\,B,\,C,\,D) = (A + B)(\bar A\, + \overline B + C)$$
$${F_3}(A,\,B,\,C,\,D) = \sum {13,15 + \sum {3,5} } $$
$${F_1}$$$$(A,\,B,\,C,\,D) = ABCD + \bar A\,\overline B \,\bar C\,\bar D$$
$${F_2}(A,\,B,\,C,\,D) = (A + B)(\bar A\, + \overline B + C)$$
$${F_3}(A,\,B,\,C,\,D) = \sum {13,15 + \sum {3,5} } $$
(a) What is the minimum size of the ROM required?
(b) Determine the data in each location of the ROM.
29
The minimum number of NAND gates required to implement the Boolean function $$A + A\overline B $$ $$ + A\overline B C$$ is equal to
30
A 'code converter' is to be designed to convert from the BCD(5421) to the normal BCD (8421). The input BCD combinations for each digit are below. A block diagram of the converter is shown in figure.
(A) draw K-map for outputs, W, X, Y, and Z.
(B) Obtain minimized expression for the outputs W, X, Y, and Z.
(A) draw K-map for outputs, W, X, Y, and Z.
(B) Obtain minimized expression for the outputs W, X, Y, and Z.
31
Two dipoles are so fed and oriented in free space that they produce the following electromagnetic waves:
$$${E_x} = 10\,{e^{j\left( {\omega t - z\pi /3} \right)}}\,\,volts/metre$$$
$$${E_y} = j\,\,10\,{e^{j\left( {\omega t - z\pi /3} \right)}}\,\,volts/metre$$$
(a) Write down the expression for the corresponding magnetic field strength vector.
(b) Calculate the frequency of the wave.
(C) Give the complete description of the polarization of the wave.
32
An antenna when radiating, has a highly directional radiation pattern. When the antenna is receiving its radiation pattern
33
A rectangular hollow metal waveguide is required to be so designed to propagate a 9375 MHz signal in its $$T{E_{10}}$$-mode that the guide-wavelength equals the cut-off wavelength. Calculate the value of 'a' (breadth or the wider dimension of the waveguide). Take b = a/2. Also, calculate the cut-off frequency of the next higher order mode.
34
In the infinite plane, y = 6 m, there exists a uniform surface charge density of (1/6000$$\pi $$) $$\mu $$C/m2. The associated electric field strength is:
35
The electric field strength at a distance point, P, due to a point charge, +q,
located at the origin, is 100 $$\mu $$V/m. If the point charge is now enclosed by a perfectly
conducting metal sheet sphere whose center is at the origin, then the
electric field strength at the point P outside the sphere becomes.
36
Copper behaves as a
37
The intrinsic impedance of a lossy dielectric medium is given by
38
The probability that an electron in a metal occupies the Fermi-level at any
temperature (> 0 K)
39
The depletion capacitance,
CJ, of an abrupt P-N junction with constant doping on
either side varies with reverse bias, VR , as
40
A zener diode works on the principle of
41
The diffusion potential across a P-N junction
42
The drift velocity of electrons in silicon
43
In a P-type silicon sample, the hole concentration is $$2.25\times10^{15}/cm^3$$.
If the
intrinsic carrier concentration is $$1.5\times10^{15}/cm^3$$ , the electron concentration is
44
The Early-Effect in a bipolar junction transistor is caused by
45
The Ebers-Moll model is applicable to
46
A BJT is said to be operating in the saturation region if
47
The breakdown voltage of a transistor with its base open is
BVCEO with
emitter open is BVCBO, then
48
If $$L\left\{ {f\left( t \right)} \right\} = {{2\left( {s + 1} \right)} \over {{s^2} + 2s + 5}}$$ then $$f\left( {{0^ + }} \right)$$ and $$f\left( \propto \right)$$ are given by ___________.
49
The third term in the taylor's series expansion of $${e^x}$$ about $$'a'$$ would be ________.
50
By reversing the order of integration $$\int\limits_0^2 {\int\limits_{{x^2}}^{2x} {f\left( {x,y} \right)dy\,dx} } $$ may be represented as ______.
51
An 'Assembler' for a microprocessor a used for
52
In a microprocessor, when a CPU is interrupted, it
53
For the 2-port network shown in Fig. determine the h-parameters. Using these parameters, calculate the output (port '2' ) $${v_2}$$, when the output port is terminated in a 3$$\Omega $$ resistance and a 1 V (DC) is applied at the input port ($${v_1}$$ = 1 V).
54
Show that the system shown in Fig. is a double integator. In other words, prove that the transfer gain is given by
$${{{V_0}\,(s)} \over {{V_s}\,(s)}} = - {1 \over {{{(CR\,s)}^2}}}$$, assume ideal OP-Amp
$${{{V_0}\,(s)} \over {{V_s}\,(s)}} = - {1 \over {{{(CR\,s)}^2}}}$$, assume ideal OP-Amp
55
Find the current-transfer-ratio, $${{I_2}}$$/$${{I_1}}$$, for the network shown below (Fig). Also, mark all branch currents.
56
A series $$R$$-$$L$$-$$C$$ circuit has a $$Q$$ of $$100$$ and an impedance of $$\left( {100 + j0} \right)\,\Omega $$ at its resonant angular frequency of $${10^7}$$ rad/sec. The values of $$R$$ and $$L$$ are: $$R=$$ ______ ohms. $$L=$$ ________Henries.
57
The current $$i(t)$$ through a $$10$$-$$\Omega $$ resistor in series with an inductance is given by
$$i(t)$$$$ = 3 + 4\sin \left( {100t + {{45}^ \circ }} \right) + 4\sin \left( {300t + {{60}^ \circ }} \right)\,\,A$$.
$$i(t)$$$$ = 3 + 4\sin \left( {100t + {{45}^ \circ }} \right) + 4\sin \left( {300t + {{60}^ \circ }} \right)\,\,A$$.
The RMS value of the current and the power dissipated in the circuit are
58
Consider a DC voltage source connected to a series R-C circuit. When the steady-state reaches, the ratio of the energy stored in the capacitor to the total energy supplied by the
voltage source, is equal to
59
A DC voltage source is connected across a series R-L-C circuit. Under steady-state conditions, the applied DC voltage drops entirely across the
60
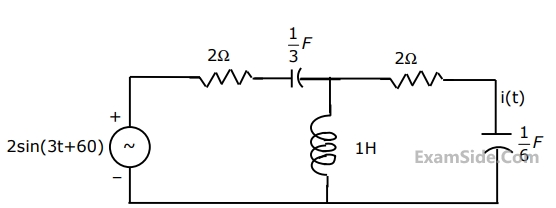
Determine the current, i(t), in the circuit given below, (Fig.), using the Thevenin's theorem.
61
The value of the resistance, R, connected across the terminals, A and B, (ref. Fig.), which will absorb the maximum power, is
62
Two 2H inductance coils are connected in series and are also magnetically coupled to each other the coefficient of coupling being 0.1.The total inductance of the combination can be
63
The final value theorem is used to find the
64
A 1.0 kHz signal is flat - top sampled at the rate of 1800 samples/sec and the samples are applied to an ideal rectangular LPF with cut - off frequency of 1100 Hz, then the output of the filter contains
65
A signal v(t)= [1+ m(t) ] cos $$({\omega _c}t)$$ is detected using a square law detector, having the characteristic $${v_0}(t) = {v^2}(t)$$. If the Fourier transform of m(t) is constant, $${M_0}$$, extending from - $${f_{m\,}}\,to\, + {f_{m\,}}$$, sketch the Fourier transform of $${v_0}(t)$$ in the frequency range-$${f_{m\,}}\, < f < {f_{m\,}}$$.
66
Non - minimum phase transfer function is defined as the transfer function
67
Let h(t) be the impulse response of a linear time invariant system. Then the response of the system for any input u(t) is
68
The transfer function of a linear system is the
69
A sinsoidal signal, v(t) = A sin(t), is applied to an ideal full-wave rectifier. Show that the Laplace Transform of the output can be written in the form, $${V_0}\left( s \right) = {A \over {{s^2} + 1}}Coth\left( {\alpha s} \right),$$
where α is a constant. Determine the value of α.
70
If L$$\left[ {f\left( t \right)} \right]$$ = $${{2\left( {s + 1} \right)} \over {{s^2} + 2s + 5}}$$, then $$f\left( {0 + } \right)\,$$ and $$f\left( \infty \right)$$ are given by
71
Match each of the items, A, B and C, with an appropriate item from 1, 2, 3, 4 and 5
A. Fourier transform of a Gaussian function
B. Convolution of a rectangular pulse with itself
C. Current through an inductor for a step input voltage
1. Gaussian function
2. Rectangular pulse
3. Triangular pulse Ramp function
4. Rump function
5. Zero