GATE ECE 1994 | GATE ECE Paper Questions with Solutions

GATE ECE 1994

GATE ECE

In order to reduce the harmonic distortion in an amplifier, its dynamic range has to be _________

A common emitter transistor amplifier has a collector current of 1.0 mA when its base current is 25 $$\mu$$A at the room temperature. It's input resistance is approximately equal to (in K$$\Omega$$) _________ .

The transit time of a current carriers through the channel of an FET decides its ____________characteristics.

In the MOSFET amplifier shown in the fig. below, the transistor has $$\mu \,\, = \,\,50,\,\,{r_d}\,\, = \,\,10\,K\Omega ,\,\,{C_{gs}}\,\, = \,\,5\,\,pF,{C_{gd}}\,\, = \,\,1pF\,\,$$ and $${C_{ds}}\,\, = \,\,2\,pF.$$ Draw a small signal equivalent circuit for the amplifier for midband frequencies and calculate its midband voltage gain.

GATE ECE 1994 Analog Circuits - FET and MOSFET Question 12 English

The frequency compensation is used in OP-Amps to increase its___________

Match the following.

GROUP-1
(A) Hartley
(B) Wein-bridge
(C) Crystal

GROUP-2
(1) Low frequency oscillator
(2) High frequency oscillator
(3) Stable frequency oscillator
(4) Relaxation oscillator
(5) Nagative Resistance oscillator

A class-A transformer coupled, transistor power Amplifier is required to deliver a power rating of the transistor should not be less than.

Find the output voltage of the following circuit assuming ideal op-amp behavior.

GATE ECE 1994 Analog Circuits - Operational Amplifier Question 11 English

The bandwidth required for the transmission of a PCM signal increases by a factor of ________ when the number of quantization levels is increased from 4 to 64.

$$v\left(t\right)\;=5\left[\cos\left(10^6\mathrm{πt}\right)\;-\;\sin\left(10^3\mathrm{πt}\right)\times\sin\left(10^6\mathrm{πt}\right)\right]$$ represents

The response of an LCR circuit to a step input is
(a) Over damped
(b) Critically damped
(c) Oscillatory

If the transfer function has

(1) poles on the negative real axis
(2) poles on the imaginary axis
(3) multiple poles on the positive real axis
(4) poles on the positive real axis
(5) multiple poles on the negative real axis

Tachometer feedback in a d.c. position control system enhances stability.

The poles of a continuous time oscillator are ___________.

If the open loop transfer function is a ratio of a numerator polynomial of degree 'm' and a denominator polynomial of degree 'n', then the integer (n-m) represents the number of

Reduce the signal flow graph shown in fig. below, to obtain another graph which does not contain the node e₅.Also, remove any self-loop from the resulting graph.

GATE ECE 1994 Control Systems - Signal Flow Graph and Block Diagram Question 3 English

Match the following with List-1 with List-2

List-1
(a) Very low response at very high frequencies.
(b) Overshoot
(c) Synchro-control transformer output

List-2
(1) Low pass systems
(2) Velocity damping
(3) Natural frequency
(4) Phase-sensitive modulation
(5) Damping ration

If G(s) is a stable transfer function, then $$F\left(s\right)=\frac1{G\left(s\right)}$$ is always a stable transfer function.

The 3-dB bandwidth of a typical second- order system with the transfer function $${{C\left( s \right)} \over {R(s)}} = {{\omega _n^2} \over {{s^2} + 2\xi {\omega _n}s + \omega _n^2}}$$, is given by

The open loop frequency response of a system at two particular frequencies are given by: 1.2 $$\angle - 180^\circ $$ and 1.0 $$\angle - 190^\circ $$. The closed loop unity feedback control system is then

Synchronous counters are _____ than the ripple counters.

A PLA can be used

A dynamic RAM consists of

In the output stage of a standard TTL, we have a diode between the emitter of the pull up transistor and the collector of the pull-down transistor. The purpose of this diode is to isolate the output node from the power supply $${V_{cc}}$$.

Match the List-1 (type of 8-bit ADC) with List-2(Minimum conversion time in clock cycles)

List - 1

A. Successive approximation
B. Dual-slope
C. Parallel Comparator

List - 2

1) 1
2) 8
3) 16
4) 256
5) 512

A Boolean function, F , given as sum of product (SOP) terms as F= $$\sum {} $$m(3,4,5,6) with A,B, and C as inputs. The function, F, can be expreeed on the Karnaugh's map shown below.

(1) What will be the minimized SOP expression for F?
(2) Implement this function on an 8 : 1 MUX.

A ring oscillator consisting of 5 inverters is running at a frequency of 1.0 MH$$_z$$. The progagation delay per gate is ______

If a pure resistance load, when connected to a lossless 75-ohm line, produces a VSWR of 3 on the line, then the load impedance can only be 25 ohms.

A load impedance (200 + j0) $$\Omega $$ is to be matched to a 50$$\Omega $$ lossless transmission line by using a quarter wave line transformer (QWT). The characteristic impedance of the QWT required is

A plane electromagnetic wave traveling along the +z-direction, has its electric field given by E_x = 2 cos $$\left( {\omega t} \right)$$ and E_y = 2 cos $$\left( {\omega t + {{90}^ \circ }} \right)$$ the wave is

A wave traveling in the $$+Z$$-direction, is the resultant of two linearly polarized components, $${E_x}\,\,\, = \,\,\,\,\,\,3$$ $$\,\,\,\,\cos \omega t$$ and $$\,{E_y}\,\,\,\, = \,\,\,2\,\cos \,\left( {\omega t + {{45}^ \circ }} \right)$$

Determine
(1) The axial ratio
(2) The angle between the major axis of the polarization ellipse and the $$+x$$-axis.

The interior of a $${{20} \over 3}\,\,cm\,\, \times \,\,{{20} \over 4}\,\,cm$$ rectangular waveguide is completely filled with a dielectric of $${ \in _r} = 4$$. Waves of free space wave-lengths shorter than .........can be propagated in the $$T{E_{11}}$$ mode.

A rectangular hollow metal waveguide of internal cross-section of $$7.366\,\,cm\,\, \times \,\,3.556\,cm$$ carries a 3 GHz signal in the $$T{E_{10}}$$-mode. Calculate the maximum power handling capability of the waveguide assuming the maximum permissible electric field inside the waveguide to be 30 kV/cm

Two spacecrafts are separated by 3000 km. Each has a paraboloidal reflector antenna of 0.85 m diameter operating at a frequency of 2 GHz with an aperture efficiency of 64%. If the space crafts A's receiver requires 1pW for a 20 dB signal-to-noise ratio, what transmitter power is required on the spacecraft B to achieve this signal-to-noise ratio?

For a dipole antenna

GATE ECE 1994 Electromagnetics - Maxwell Equations Question 45 English

A p-type silicon sample has a higher conductivity compared to an n-type sample having the same dopant concentration.

A small concentration of minority carries is injected into a homogeneous semiconductor crystal at one point. An electric field of 10 V/cm is applied across the crystal and this moves the minority carriers a distance of 1 cm is 20 $$\mu$$ sec. The mobility (in cm²/volt-sec) will be

Channel current is reduced on application of a more positive voltage to the gate of a depletion mode n-channel MOSFET.

The transit time of the current carriers through the channel of an FET decides its ____________characteristics.

The threshold voltage of an n-channel MOSFET can be increased by

The following system of equations
$${{x_1} + {x_2} + {x_3} = 3}$$
$${{x_1} - {x_3} = 0}$$
$${{x_1} - {x_2} + {x_3} = 1}$$ has

The rank of $$\left( {m \times n} \right)$$ matrix $$\left( {m < n} \right)$$ cannot be more then

The function $$y = {x^2} + {{250} \over x}$$ at $$x=5$$ attains

$$y = {e^{ - 2x}}$$ is a solution of the differential equation $$\,{y^{11}} + {y^1} - 2y = 0$$

Match each of the items $$A, B, C$$ with an appropriate item from $$1, 2, 3, 4$$ and $$5$$

List-$${\rm I}$$
$$(P)$$ $${a_1}{{{d^2}y} \over {d{x^2}}} + {a_2}y{{dy} \over {dx}} + {a_3}y = {a_4}$$
$$(Q)$$ $${a_1}{{{d^2}y} \over {d{x^3}}} + {a_2}y = {a_3}$$
$$(Q)$$ $${a_1}{{{d^2}y} \over {d{x^2}}} + {a_2}x{{dy} \over {dx}} + {a_3}{x^2}y = 0$$

List-$${\rm II}$$
$$(1)$$ Non-linear differential equation
$$(2)$$ Linear differential equation with constants coefficients
$$(3)$$ Linear homogeneous differential equation
$$(4)$$ Non-linear homogeneous differential equation
$$(5)$$ Non-linear first order differential equation

Write down the sequence of Instructions which are actually (till HLT instruction), if the program begins with the location 1FF5H.

GATE ECE 1994 Microprocessors - Instruction Set and Programming with 8085 Question 1 English

The circuit shown in the figure, is initially in its steady state. Switch is opened at t = 0.
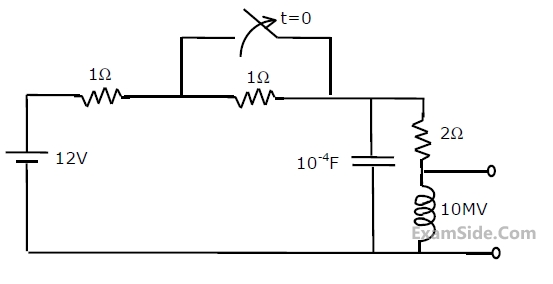
(1) Determine the initial voltage, V_C(0^-), across the capacitor, and the initial current, i_L(0^-) , through the indicator.
(2) Calculate the voltage, V_L(t) , across the inductance for t > 0.

GATE ECE 1994 Network Theory - Transient Response Question 11 English

A series LCR circuit consisting of $$R = 10\Omega $$, $$\left| {{X_L}} \right|\,\,\, = 20\Omega $$ and $$\left| {{X_C}} \right|\,\,\, = 20\Omega $$, is connected across an a.c. supply of $$200V$$ rms. The rms voltage across the capacitor is

Calculate the frequency at which zero- transmission is obtained from the Wien- bridge shown in Fig.

GATE ECE 1994 Network Theory - Sinusoidal Steady State Response Question 16 English

Assuming that the amplifier shown in the Fig., below, is a voltage-controlled voltage source, show that the voltage transfer function of the network is given by
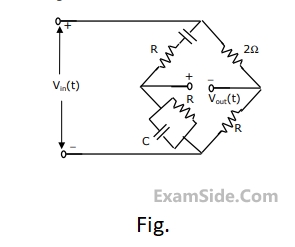
$$T(s) = {{{V_2}\,(s)} \over {{V_1}\,(s)}} = \,{K \over {{s^2} + \,(3 - K)\,s + 1}}$$

GATE ECE 1994 Network Theory - Two Port Networks Question 15 English

A ramp voltage, v(t) = 100 t Volts, is applied to an RC differentiating circuit with R = $$5k\Omega$$ and C = $$4\mu F$$.The maximum output voltage is

The condition, that a 2-port network is reciprocal, can be expressed in terms of its ABCD parameters as ...............

Write down the mesh equation of the following network in terms of i₁(t) and i₂(t).Derive the differential equation for i₁(t) from these and solve it.

GATE ECE 1994 Network Theory - Sinusoidal Steady State Response Question 48 English

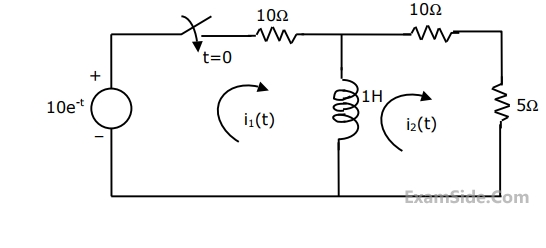
A generator of internal impedance, Z_G, delivers maximum power to a load impedance, Z_L, only if Z_L = ................

The laplace transform of a unit ramp function starting at t=a, is

Indicate whether the following statement is TRUE/FALSE: Give reason for your answer.

If G(s) is a stable transfer function, then $$F\left( s \right) = {1 \over {G\left( s \right)}}$$ is always a stable transfer function.

Match each of the items A, B and C with an appropriate item from 1, 2, 3, 4 and 5.

List - 1
(A) $${a_1}{{{d^{2y}}} \over {d{x^2}}} + {a_2}y{{dy} \over {dx}} + {a_3}y = {a_4}$$
(B) $${a_1}{{{d^3}y} \over {d{x^3}}} + {a_2}y = {a_3}$$
(C) $$\eqalign{ & {a_1}{{{d_2}y} \over {d{x_2}}} + {a_2}x{{dy} \over {dx}} + {a_3}\,{x^2}y = 0 \cr & \cr} $$

List - 2
(1) Non linear differential equation.
(2) Linear differential equation with constant coefficients.
(3) Linear homogeneous differential equation.
(4) Non - Linear homogeneous differential equation.
(5) Non - linear first order differential equation.

Increased pulse-width in the flat-top sampling, leads to

GATE ECE 1994 Signals and Systems - Sampling Question 29 English

A signal, f(t) = $${e^{ - at}}$$ u(t), where u(t) is the unit step function, is applied to the input of a low-pass filter having $$\left| {H(\omega )} \right| = {b \over {\sqrt {{\omega ^2} + {b^2}} }}$$.

Calculate the value of the ratio, $${a \over b}$$, for which 50% of the input signal energy is transferred to the output.

The Fourier Series of an odd periodic function, contains only