GATE ECE 2015 Set 2
GATE ECE
1
If the circuit shown has to function as a clamping circuit, which one of the following
conditions should be satisfied for sinusoidal signal of period T?


2
The diode in the circuit given below has
VON = 0.7V
but is ideal otherwise. The current (in mA) in the 4kΩ resistor is __________.


3
In the ac equivalent circuit shown, the two BJTs are biased in active region and have identical
parameters with β >> 1. The open circuit small signal voltage gain is approximately _______.


4
In the circuit shown, VO = VOA for switch SW in position A and V0= VOB for SW in position B. Assume that the opamp is ideal.

The value of $${{{V_{OB}}} \over {{V_{OA}}}}$$ is _____

5
In the bistable circuit shown, the ideal opamp has saturation levels of $$ \pm 5V.$$ The value of R1 (in k$$\Omega $$ ) that gives a hystersis width of 500 mV is ______


6
For the voltage regulator circuit shown, the input voltage (Vin) is 20V $$ \pm $$ 20% and the regulated output voltage (Vout) is 10 V. Assume the opamp to be ideal . For a load RL drawing 200 mA, the maximum power dissipation in Q1 (in Watts) is ______.


7
Assuming that the op-amp in the circuit shown below is ideal, the output voltage V0 (in volts)


8
A zero mean white Gaussian noise having power spectral density $${{{N_0}} \over 2}$$ is passed through an $$ LTI $$
filter whose impulse response $$h(t)$$ is shown in the figure. The variance of the filtered noise at $$t = 4$$ is


9
$$\mathop {\left\{ {{X_n}} \right\}}\nolimits_{n = - \infty }^{n = \infty } $$ is an independent and identically distributed (i.i.d) random process with $${X_n}$$ equally likely to be $$+1$$ or $$-1$$. $$\mathop {\left\{ {{Y_n}} \right\}}\nolimits_{n = - \infty }^{n = \infty } \,$$ is another random process obtained as $${Y_n} = {X_n} + 0.5{X_{n - 1}}.\,\,\,$$
The autocorrelation function of $$\mathop {\left\{ {{Y_n}} \right\}}\nolimits_{n = - \infty }^{n = \infty } $$, denoted by $${r_y}\left[ K \right],$$ is
The autocorrelation function of $$\mathop {\left\{ {{Y_n}} \right\}}\nolimits_{n = - \infty }^{n = \infty } $$, denoted by $${r_y}\left[ K \right],$$ is
10
Let $$X \in \left\{ {0,1} \right\}$$ and $$Y \in \left\{ {0,1} \right\}$$ be two independent binary random variables.
If $$P\left( {X\,\, = 0} \right)\,\, = p$$ and $$P\left( {Y\,\, = 0} \right)\,\, = q,$$ then $$P\left( {X + Y \ge 1} \right)$$ is equal to
11
A sinusoidal signal of amplitude A is quantized by a uniform quantizer. Assume that the signal
utilizes all the representation levels of the quantizer. If the signal to quantization noise ratio is 31.8
dB, the number of levels in the quantizer is _________ .
12
Consider a binary, digital communication system which uses pulses g (t) and − g (t)for transmitting bits over an AWGN channel. If the receiver uses a matched filter, which one of the following pulses will give the minimum probability of bit error?
13
The state variable representation of a system is given as
$$$\eqalign{
& \mathop x\limits^ \bullet = \left[ {\matrix{
0 & 1 \cr
0 & { - 1} \cr
} } \right]x;x\left( 0 \right) = \left[ {\matrix{
1 \cr
0 \cr
} } \right] \cr
& y = \left[ {\matrix{
0 & 1 \cr
} } \right]x \cr} $$$
The response y(t) is
14
By performing cascading and/or summing/differencing operations using transfer function
blocks G1(s) and G2(s), one CANNOT realize a transfer function of the form
15
For the signal flow graph shown in the figure, the value of $$\frac{\mathrm C\left(\mathrm s\right)}{\mathrm R\left(\mathrm s\right)}$$ is


16
A unity negative feedback system has an open–loop transfer function $$G\left(s\right)=\frac K{s\left(s+1\right)}$$.The
gain K for the system to have a damping ratio of 0.25 is _____________.
17
The output of a standard second–order system for a unit step input is given as $$$y\left(t\right)=1-\frac2{\sqrt3}e^{-t}\cos\left(\sqrt3t\;-\;\frac{\mathrm\pi}6\right)$$$ The transfer function of the system is
18
The transfer function of a mass-spring damper system is given by
$${\rm{G(s) = }}{1 \over {M{s^2} + Bs + K}}$$
The frequency response data for the system are given in the following table.
 The unit step response of the system approaches a steady state value of ______.
The unit step response of the system approaches a steady state value of ______.
 The unit step response of the system approaches a steady state value of ______.
The unit step response of the system approaches a steady state value of ______.
19
A function of Boolean variables X,Y and Z is expressed in terms of the min-terms as F(X, Y, Z)=$$\sum\limits_{}^{} {} $$m(1,2,5,6,7) Which one of the product of sums given below is equal to the funtion F(X, Y, Z)?
20
In the figure shown, the output ܻ is required to be ܻ Y=AB+ $$\overline C $$$$\overline D $$. The gates G1 and G2 must be,
respectively,


21
A 1-to-8 demultiplexer with data input D$$_{in}$$ , address inputs S$$_{0}$$, S$$_{1}$$, S$$_{2}$$ (with S$$_{0}$$ as the LSB) and $${\overline Y _0}$$ to $${\overline Y _7}$$
as the eight demultiplexed outputs, is to be designed using two 2-to-4 decoders (with enable input $$\overline E $$ and address inputs A$$_{0}$$ and A$$_{1}$$) as shown in the figure. $${D_{in}}$$, S$$_{0}$$, S$$_{1}$$and S$$_{2}$$ are to be
connected to P, Q, R and S, but not necessarily in this order. The respective input connections to P,
Q, R, and S terminals should be


22
A mod-n counter using a synchronous binary up-counter with synchronous clear input is shown in the figure. The value of n is _______.


23
The figure shows a binary counter with synchronous clear input. With the decoding logic shown,
the counter works as a


24
An air-filled rectangular waveguide of internal dimension $$a\,\,cm\,\, \times \,\,b\,\,cm$$ (a > b) has a cutoff frequency of 6 GHz for the dominant $$T{E_{10}}$$ mode. For the same waveguide, if the cutoff frequency of the $$T{E_{11}}$$ mode is 15 GHz, the cutoff frequency of the $$T{E_{01}}$$ mode in GHz is _____________
25
The electric field of a uniform plane electromagnetic wave is
$$$\vec E = \left( {{{\overrightarrow a }_x} + j4{{\overrightarrow a }_y}} \right)\exp \left[ {j\left( {2\pi \times {{10}^7}t - 0.2z} \right)} \right]$$$
The polarization of the wave is
26
The electric field intensity of a plane wave propagating in a lossless non-magnetic medium is given by the following expression
$$\overrightarrow E \left( {z,t} \right) = {\widehat a_x}5\cos \left( {2\pi \times {{10}^9}t + \beta z} \right)$$ $$$ + {\widehat a_y}3\cos \left( {2\pi \times {{10}^9}t + \beta z - {\pi \over 2}} \right)$$$
$$\overrightarrow E \left( {z,t} \right) = {\widehat a_x}5\cos \left( {2\pi \times {{10}^9}t + \beta z} \right)$$ $$$ + {\widehat a_y}3\cos \left( {2\pi \times {{10}^9}t + \beta z - {\pi \over 2}} \right)$$$
The type of the polarization is
27
Two half-wave dipole antennas placed as shown in the figure are excited with sinusoidally varying currents of frequency 3 MHz and phase shift of $$\pi /2$$ between them (the element at the origin leads in phase). If the maximum radiated E-field at the point P in the x-y plane occurs at an azimuthal angle $${60^ \circ }$$, the distance d (in meters) between the antennas is ___________ .


28
In a source free region in vacuum, if the electrostatic potential
$$\varphi\;=\;2x^2\;+y^2+cz^2$$ , the value of
constant c must be ________________.
29
An n–type silicon sample is uniformly illuminated with light which generates 1020
electron hole pairs per cm3
per second. The minority carrier lifetime in the sample is 1 $$\mathrm\mu$$s.In the
steady state, the hole concentration in the sample is approximately
10x , where x is an integer.
The value of x is __________________
30
A piece of silicon is doped uniformly with phosphorous with a doping concentration of
$$10^{16}/cm^2$$. The expected value of mobility versus doping concentration for silicon assuming
full dopant ionization is shown below. The charge of an electron is $$1.6\;\times\;10^{-19}\;C$$.
The
conductivity
(in S cm-1) of the silicon sample at 300 K is _________________.


31
A dc voltage of 10V is applied across an n–type silicon bar having a rectangular cross–section
and a length of 1cm as shown in figure. The donor doping concentration ND and the mobility of electrons $$\mu$$n are $$10^{16}$$ cm-3 and 1000 cm2 V-1s-1, respectively. The average time (in $$\mu$$s)
taken by the electrons to move from one end of the bar to other end is _______________.


32
In a MOS capacitor with an oxide layer thickness of 10 nm, the maximum depletion layer thickness is 100 nm. The permittivities of the semiconductor and the oxide layer are $${\varepsilon _s}$$ and $${\varepsilon _{os}}$$ respectively. Asuuming $${\varepsilon _s}/{\varepsilon _{ox}} = 3$$ , the ratio of the maximum capacitance to the minimum capacitance of this MOS capacitor is________
33
The value of $$'x'$$ for which all the eigenvalues of the matrix given below are real is $$\left[ {\matrix{
{10} & {5 + j} & 4 \cr
x & {20} & 2 \cr
4 & 2 & { - 10} \cr
} } \right]$$
34
The value of the integral $$\int_{ - \infty }^\infty {12\,\,\cos \left( {2\pi t} \right){{\sin \left( {4\pi t} \right)} \over {4\pi t}}} dt\,\,$$ is __________.
35
Let the random variable $$X$$ represent the number of times a fair coin needs to be tossed till two consecutive heads appear for the first time. The expectation of $$X$$ is ________.
36
Let $$\,\,X \in \left\{ {0,1} \right\}\,\,$$ and $$\,\,Y \in \left\{ {0,1} \right\}\,\,$$ be two independent binary random variables. If $$\,\,P\left( {X\,\, = 0} \right) = p\,\,$$ and $$\,\,P\left( {Y\,\, = 0} \right) = q\,\,$$, then $$P\left( {X + Y \ge 1} \right)$$ is equal to
37
Ram and Ramesh appeared in an interview for two vacancies in the same department. The probability of Ram's selection is $$1/6$$ and that of Ramesh is $$1/8$$. What is the probability that only one of them will be selected?
38
The general solution of the differential equation $$\,\,{{dy} \over {dx}} = {{1 + \cos 2y} \over {1 - \cos 2x}}\,\,$$ is
39
Consider the differential equation $$\,\,{{dx} \over {dt}} = 10 - 0.2\,x$$ with initial condition $$x(0)=1.$$ The response $$x(t)$$ for $$t > 0$$ is
40
Let $$f\left( z \right) = {{az + b} \over {cz + d}}.$$ If $$f\left( {{z_1}} \right) = f\left( {{z_2}} \right)$$ for all $${z_1} \ne {z_2}.\,\,a = 2,\,\,b = 4$$ and $$C=5,$$ then $$d$$ should be equal to
41
If $$C$$ denotes the counter clockwise unit circle. The value of the contour integral $${1 \over {2\pi i}}\oint\limits_c {{\mathop{\rm Re}\nolimits} \left\{ z \right\}dz} $$ is __________.
42
The bilateral Laplace transform of a function
$$f\left( t \right) = \left\{ {\matrix{ 1 & {if\,\,a \le t \le b} \cr 0 & {otherwise} \cr } } \right.$$ is
$$f\left( t \right) = \left\{ {\matrix{ 1 & {if\,\,a \le t \le b} \cr 0 & {otherwise} \cr } } \right.$$ is
43
In an 8085 microprocessor, which one of the following instructions changes the content of the accumulator?
44
The voltage (VC) across the capacitor (in Volts) In the network shown is ________.


45
The 2-port admittance matrix of the circuit shown is given by
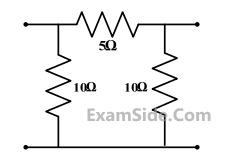

46
In the circuit shown, the initial voltages across the capacitors
C1 and C2
are 1 V and 3 V,
respectively. The switch is closed at time t = 0. The total energy dissipated (in Joules) in the
resistor R until steady state is reached is _______________.
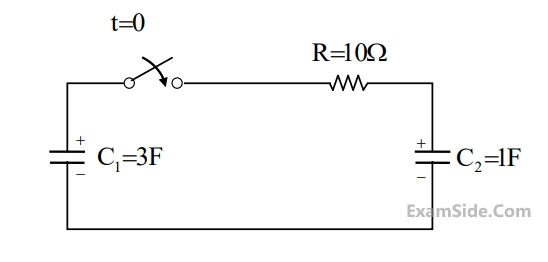

47
In the circuit shown, the Norton equivalent resistance (in Ω) across terminals a–b is ___________.

48
Let x(t) = a s(t) +s(-t) with s(t) = $$\beta {e^{ - 4t}}u\left( t \right)$$, where u(t) is unit step function. If the bilateral Laplace transform of x(t) is
$$$X\left( S \right)\, = {{16} \over {{S^2} - 16}} - 4 < {\mathop{\rm Re}\nolimits} \left\{ s \right\} < 4;$$$
Then the value of β is ______.
49
Two casual discrete-time signals $$x\left[ n \right]$$ and $$y\left[ n \right]$$ =$$\sum\limits_{m = 0}^n x \left[ m \right]$$. If the z-transform of y$$\left[ n \right]$$=$${2 \over {z{{(z - 1)}^2}}}$$ , the value of $$x\left[ 2 \right]$$ is _____________________
50
Input x(t) and output y(t) of an LTI system are related by the differential equation y"(t) - y'(t) - 6y(t) = x(t). If the system is neither causal nor stable, the imulse response h(t) of the system is
51
The output of a standrad second-order system for a unit step input is given as $$y(t) = 1 - {2 \over {\sqrt 3 }}{e^{ - t}}\cos \left( {\sqrt 3 t - {\pi \over 6}} \right)$$.
The transfer function of the system is
52
The value of the integral $$\int_{ - \infty }^\infty {12\,\cos (2\pi )\,{{\sin (4\pi t)} \over {4\pi t}}\,dt\,} $$ is
53
The signal $$\cos \left( {10\pi t + {\pi \over 4}} \right)$$ is ideally sampled at a sampling frequency of 15 Hz. The sampled signal is passed through a filter with impulse response $$\,\left( {{{\sin \left( {\pi t} \right)} \over {\pi t}}} \right)\,\cos \left( {40\pi t - {\pi \over 2}} \right).$$ The filter output is
54
The bilateral Laplace transform of a function $$f\left( t \right) = \left\{ {\matrix{
{1\,if\,a \le t \le b} \cr
{0\,otherwise} \cr
} } \right.$$ is