Introducing a resistor in the emitter of a common amplifier, stabilizes the dc operating point against variations in

In the circuit shown in the figure assume that the transistor is in the active region. It has a large β and its base Emitter voltage is 0.74. The value of I_c is

For the amplifier of given figure,
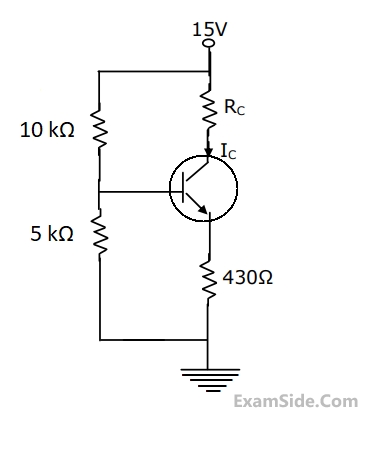
$${I_C}\, = \,1.3\,mA,\,{R_C}\, = \,2\,k\Omega ,\,{R_E}\, = \,500\,\Omega ,$$
$${V_T}\, = \,26\,mV,\,\beta \, = \,100,\,{V_{CC}}\, = \,15V,$$
$${V_s}\, = \,0.01\,\sin \left( {\omega t} \right)\,V\,and\,{C_b}\, = \,{C_C}\, = \,10\,\mu F.$$

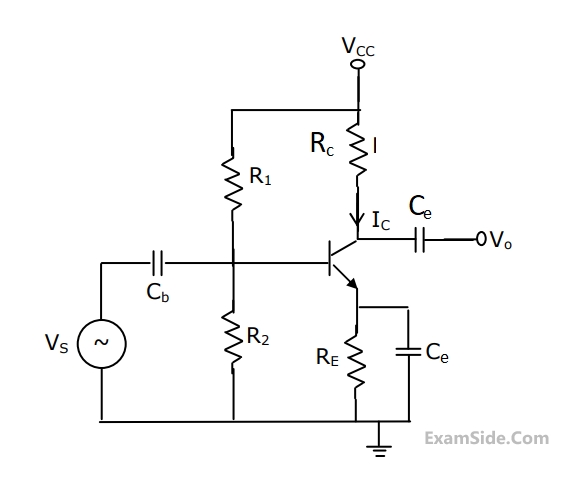
(a)What is the small-signal voltage gain, $${A_V} = {V_0}/{V_s}?$$
(b)What is the approximate $${A_{v,}}\,\,if\,\,{C_e}\,\,$$ is removed?
(c)What will $${V_0}\,be\,if\,{C_b}$$ is short circuited?

The current gain of a bipolar transistor drops at high frequencies because of

In the circuit of figure V₀ is

If the Op-Amp in the figure, is ideal, than V₀ is

The most commonly used Amplifier in sample and hold circuit is

If the Op-Amp in the figure has an input offset voltage of 5 mV and an open-loop voltage gain of 10,000, V₀ will be

In a digital communication system employing Frequency Shift Keying (FSK), the 0 and 1 bit are represented by sine waves of 10 KHz and 25 KHz respectively. These waveforms will be orthogonal for a bit interval of

In an FM system, a carrier of 100 MHz is modulated by a sinusoidal signal of 5 KHz. The bandwidth by Carson’s approximation is 1 MHz. If y(t) = (modulated waveform)³, then by using Carson’s approximation, the bandwidth of y(t) around 300 MHz and the and the spacing of spectral components are, respectively.

For the linear, time-invariant system whose block diagram is shown in Fig. with input x(t) and output y(t),
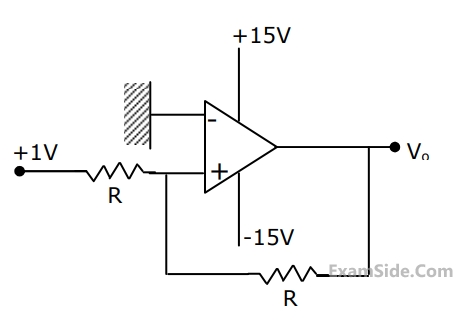
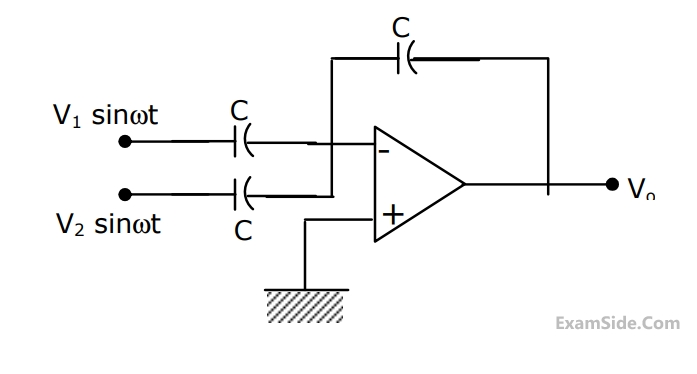
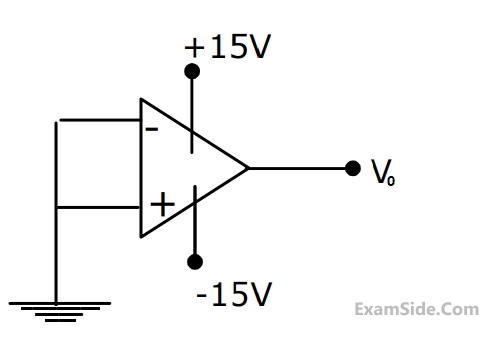
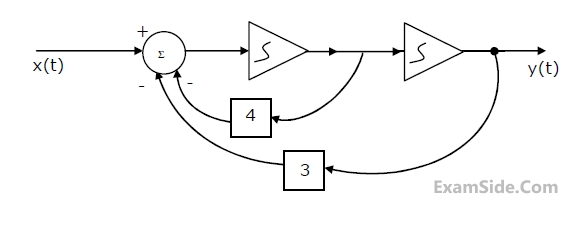
(a) Find the transfer function.
(b) For the step response of the system [i.e. find y(t) when x(t) is a unit step function and the initial conditions are zero]
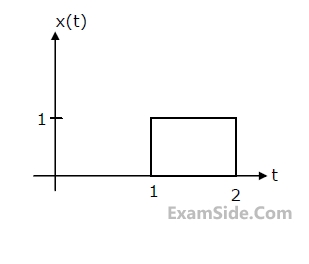
(c) Find y(t), if x(t) is as shown in Fig. and the initial conditions are zero.

A linear time invariant system has an impulse response e^2t, t > 0. If the initial conditions are zero and the input is e^3t, the output for t > 0 is

An amplifier with resistive negative feedback has two left half-plane poles in its open-loop transfer function. The amplifier

The block diagram of a feedback system is shown in Figure.
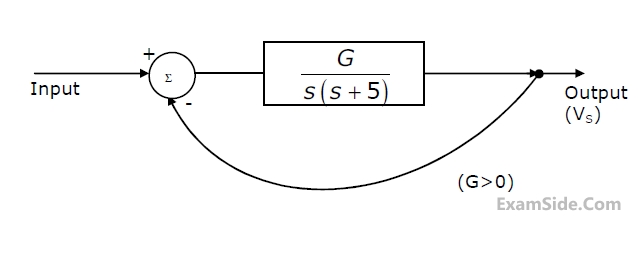
(a) Find the closed loop transfer function.
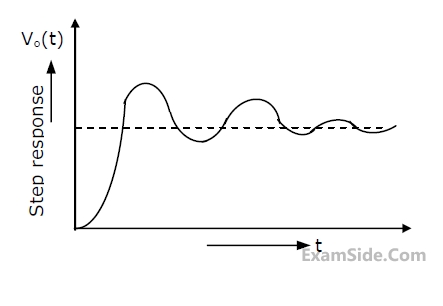
(b) Find the minimum value of G for which the step response of the system would exhibit an overshoot, as shown in Figure.
(c) For G equal to twice this minimum value, find the time period T indicated in Figure.

A system described by the transfer function $$$H\left(s\right)=\frac1{s^3+\alpha s^2+ks+3}$$$ is stable. The constraints on $$\alpha$$ and k are,

A certain linear, time-invariant system has the state and output representation shown below: $$$\eqalign{ & \left[ {\matrix{ {\mathop {{x_1}}\limits^ \bullet } \cr {\mathop {{x_2}}\limits^ \bullet } \cr } } \right] = \left[ {\matrix{ { - 2} & 1 \cr 0 & { - 3} \cr } } \right]\left[ {\matrix{ {{x_1}} \cr {{x_2}} \cr } } \right] + \left[ {\matrix{ 1 \cr 0 \cr } } \right]u \cr & y = \left( {\matrix{ 1 & 1 \cr } } \right)\left[ {\matrix{ {{x_1}} \cr {{x_2}} \cr } } \right] \cr} $$$
(a) Find the eigen values (natural frequencies) of the system.
(b)If u(t)=$$\delta \left( t \right)$$ and x₁(0⁺)=x₂(0⁺)=0, find x₁(t),x₂(t) and y(t), for t>0.
(c)When the input is zero, choose initial conditions $${x_1}\left( {{0^ + }} \right)$$ and $${x_2}\left( {{0^ + }} \right)$$ such that $$y\left( t \right) = A{e^{ - 2t}}$$ for t>0

In the figure, the J and K inputs of all the four Flip-Flops are made high. The frequency of the signal at output Y is

The number of comparators in 4-bit flash ADC is

For the 4 bit DAC shown in Figure, the output voltage $${V_0}$$ is

A sequential circuit using D flip-flop and logic gates is shown in the figure, where X and Y are the inputs and Z is the output. The circuit is

For the logic circuit shown in Figure, the required input condition (A, B, C) to make the output (X)=1.

For the logic circuit shown in the figure, the simplified Boolean expression for the output Y is

The operating conditions (ON = 1, OFF = 0) of three pumps (x,y,z) are to be monitored. x = 1 implies that pump X is on. It is required that the indicator (LED) on the panel should glow when a majority of the pumps fail.

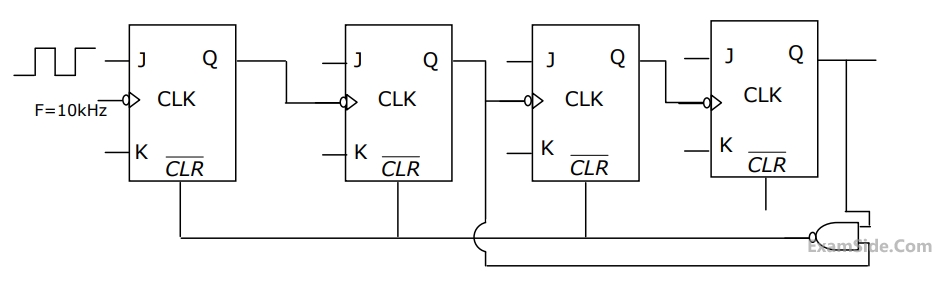
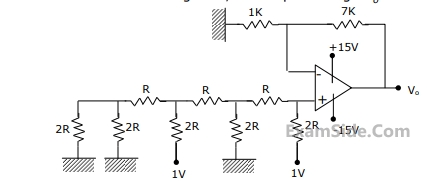
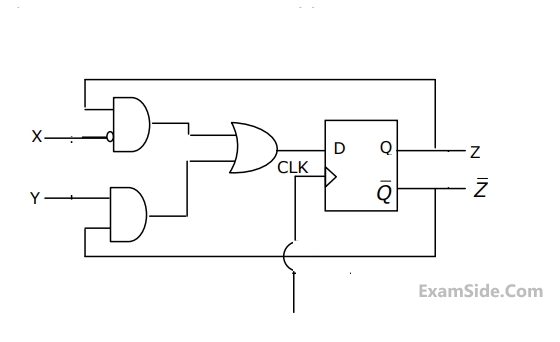
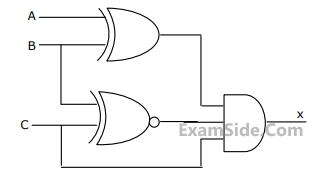
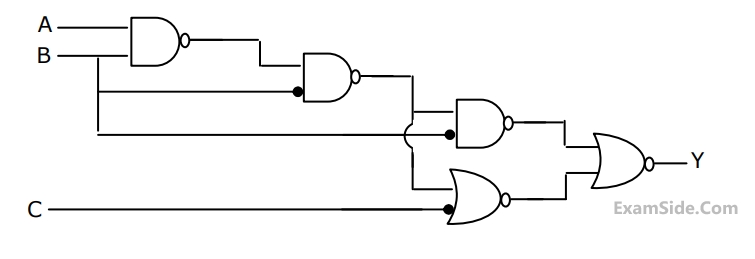
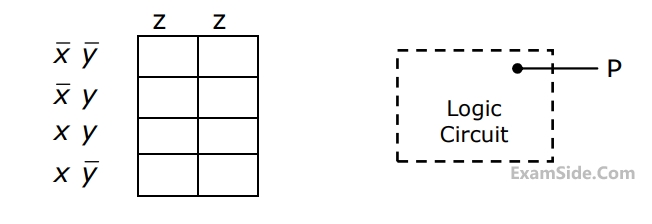
(a) Enter the logical values in the K-map in the format shown in figure 3(a). Derive the minimal Boolean sum-of-products expression whose output is zero when a majority of the pumps fail.
(b) The above expression is implemented using logic gates, and point P is the output of this circuit, as shown in figure 3(b). P is at 0 V when a majority of the pumps fails and is at 5 V otherwise. Design a circuit to drive the LED using this output. The current through the LED should be 10 mA and the voltage drop across it is 1V. Assume that P can source or sink 10 mA and a 5 V supply is available.

A TEM wave is incident normally upon a perfect conductor. The E and H fields at the boundary will be respectively

The magnitudes of the open-circuit and short-circuit input impedances of a transmission line are 100$$\Omega \,$$ and 25$$\Omega \,$$ respectively. The characteristic impedance of the line is

A uniform plane wave in air impinges at 45° angle on a lossless dielectric material with dielectric constant $${\varepsilon _r}$$. The transmitted wave propagates in a 30° direction with respect to the normal. The value of $${\varepsilon _r}$$ is

The three regions shown in Fig. are all lossless and non-magnetic. Find

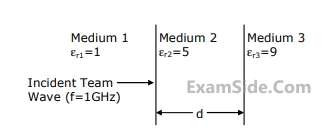
(a) Wave impedance in mediums 2 and 3.
(b) d such that medium 2 acts as a quarter wave $$(\lambda /40$$)transformer.
(c) Reflection coefficient $$(\Gamma )$$ and voltage standing wave ratio (VSWR) at the interface of the medium 1 and 2, when $$d = \lambda /4$$.

A rectangular waveguide has dimensions $$1\,\,cm\,\, \times \,\,0.5\,\,cm$$. Its cut-off frequency is

For an 8 feet (2.4 m) parabolic disk antenna operating at 4 GHz, the minimum distance required for far field measurement is closest to

The half-power beam widths (HPBW) of an antenna in the two orthogonal planes are $${100^ \circ }$$ and $${60^ \circ }$$ respectively. The directivity of the antenna is approximately equal to

If the diameter of a $$\lambda /2$$ dipole antenna is increased from $$\lambda /100$$ to $$\lambda /50$$ then is

The eigen values of the matrix $$\left[ {\matrix{ 2 & { - 1} & 0 & 0 \cr 0 & 3 & 0 & 0 \cr 0 & 0 & { - 2} & 0 \cr 0 & 0 & { - 1} & 4 \cr } } \right]$$ are

$$\int\limits_0^{{\raise0.5ex\hbox{$\scriptstyle \pi $} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 2$}}} {\int\limits_0^{{\raise0.5ex\hbox{$\scriptstyle \pi $} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 2$}}} {\sin \left( {x + y} \right)dx\,dy} } $$

If $$\,\,\,$$ $$L\left\{ {f\left( t \right)} \right\} = {{s + 2} \over {{s^2} + 1}},\,\,L\left\{ {g\left( t \right)} \right\} = {{{s^2} + 1} \over {\left( {s + 3} \right)\left( {s + 2} \right)}},$$
$$h\left( t \right) = \int\limits_0^t {f\left( T \right)} g\left( {t - T} \right)dT$$
then $$L\left\{ {h\left( t \right)} \right\}$$ is _______________.

In the 8085 microprocessor, the RST6 instruction transfers the program execution to the following location

The number of hardware interrupts (which require an external signal to interrupt) present in an 8085 microprocessor are

The network $$N$$ in Fig. consists only of two elements: a resistor of $$1\Omega $$ and an inductor of L Henry. $$A$$ $$5$$ $$V$$ source is connected at the input at $$t\, = \,0$$ seconds. The inductor current is zero at $$t\, = \,0$$. The output voltage is found to be $$5{e^{ - 3t}}\,\,V,$$ for $$t\, = \,0$$.

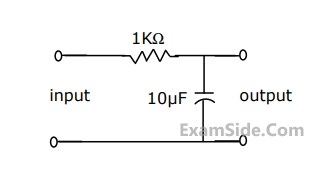
(a) Find the voltage transfer function of the network.
(b) Find L, and draw the configuration of the network.
(c) Find the impulse response of the network.

In Fig., the steady state output voltage corresponding to the input voltage $$\left( {3 + 4\sin \,\,100\,t} \right)$$ $$V$$ is

For the circuit in Fig. Which is in steady state,

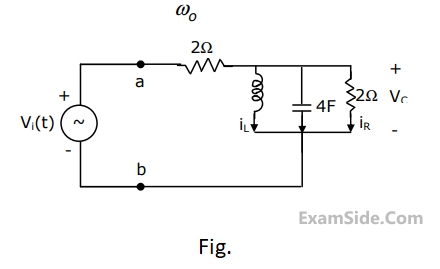
(a)Find the frequency $${\omega _0}$$ at which the magnitude of the impedance across terminals a, b reaches maximum.

(b) Find the impedance across a, b at the frequency $${\omega _0}$$.

(c) If $${v_i}\left( t \right) = V\,\,\sin \left( {{\omega _0}t} \right),$$ find $${i_L}\left( t \right),\,\,{i_c}\left( t \right),{i_R}\left( t \right).$$

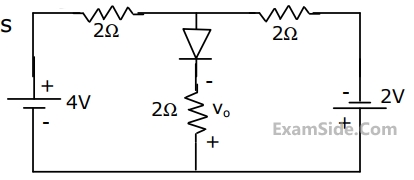
In the circuit of Fig., the value of the voltage source E is

For the circuit in Fig. the voltage V₀ is

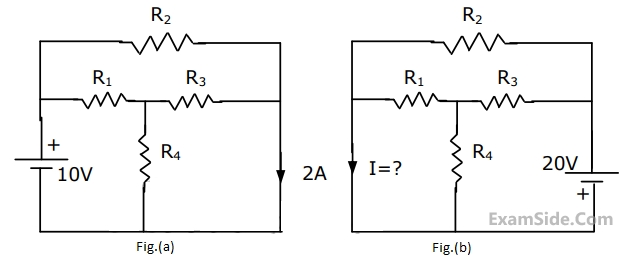
Use the data of Fig.(a). The current i in the circuit of Fig.(b) is

The circuit of Fig. represents a

For the circuit in Fig., write the state equations using v_c and i_L as state variables.

For the circuit in Fig.

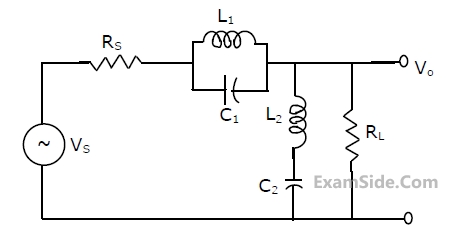
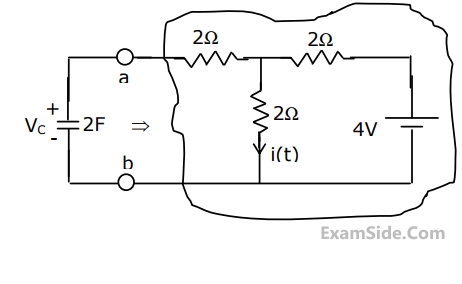
(a) Find the Thevenin equivalent of the sub circuit faced by the capacitor across the terminals a, b.

(b) Find $$v_c\left(t\right),\;t>0,\;given\;v_c(0)\;=\;0.$$

(c) Find i(t), t>0.

In the circuit of Fig., the votage v(t) is

Given that $$L\left[ {f\left( t \right)} \right]\, = \,$$ $${{s + 2} \over {{s^2} + 1}},$$ $$$L\left[ {g\left( t \right)} \right] = {{{s^2} + 1} \over {\left( {s + 3} \right)\left( {s + 2} \right)}},$$$ $$$h\left( t \right) = \int\limits_0^t {f\left( \tau \right)\,g\left( {t - \tau } \right)\,d\tau ,} $$$ $$L\left[ {h\left( t \right)} \right]$$ is

A system with an input x(t) and an output y(t) is described by the relation: y(t) = t x(t). This system is

The Fourier Transform of the signal $$x(t) = {e^{ - 3{t^2}}}$$ is of the following form, where A and B are constants:

A linear time invariant system has an impulse response $${e^{2t}},\,\,t\, > \,0.$$ If the initial conditions are zero and the input is $${e^{3t}}$$, the output for $$t\, > \,0$$ is

Let u(t) be the unit step function. Which of the waveforms in Fig.(a) -(d) corresponds to the convolution of $$\left[ {u\left( t \right)\, - \,u\left( {t\, - \,1} \right)} \right]$$ with $$\left[ {u\left( t \right)\, - \,u\left( {t\, - \,2} \right)} \right]$$ ?

The Hilbert transform of $$\left[ {\cos \,{\omega _1}t + \,\sin {\omega _2}t\,} \right]$$ is

For the linear, time-invariant system whose block diagram is shown in Fig.(a), with input x(t) and output y(t).

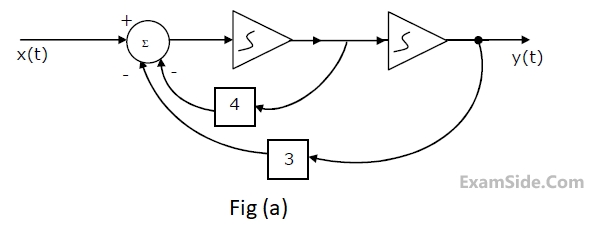
(a) Find the transfer function.
(b) For the step response of the system [i.e. find y(t) when x(t) is a unit step function and the initial conditions are zero]
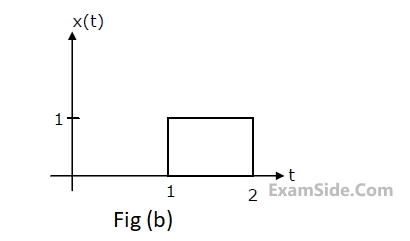
(c) Find y(t), if x(t) is as shown in Fig.(b), and the initial conditions are zero.

A system has a phase response given by $$\phi \,(\omega )$$ where $$\omega $$ is the angular frequency. The phase delay and group delay at $$\omega $$ = $${\omega _0}$$ are respectively given by

A band limited signal x(t) with a spectrum X(f) as shown in Fig. a is processed as shown in Fig.b. p(t) is a periodic train of impulses as in Fig. c. The ideal band pass filter has a pass band from 26 KHz to 34 KHz.
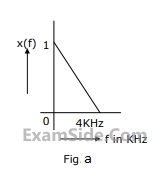
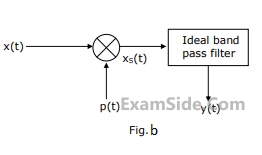
(a) Calculate the Fourier series coefficients $${c_n}$$ in the Fourier expansion of p(t) in form $$p(t) = \sum\limits_{n = - \infty }^{ + \infty } {{c_n}} \,\exp \,\,(j\,n\,2\pi \,t/T)$$.
(b) Find the Fourier Transform of p(t).
(c) Obtain and sketch the spectrum of $${x_s}(t)$$.
(d) Obtain and sketch the spectrum of y(t).