In the silicon BJT circuit shown below, assume that the emitter area of transistor Q₁ is half that of transistor Q₂.The value of current I₀ is approximately

The amplifier circuit shown below uses a silicon transistor. The capacitors C_C and C_E can be assumed to be short at signal frequency and the effect of output resistance r₀ can be ignored. If C_E is disconnected from the circuit, which one of the following statements is TRUE?

Consider the common emitter amplifier shown below with the following circuit parameters:

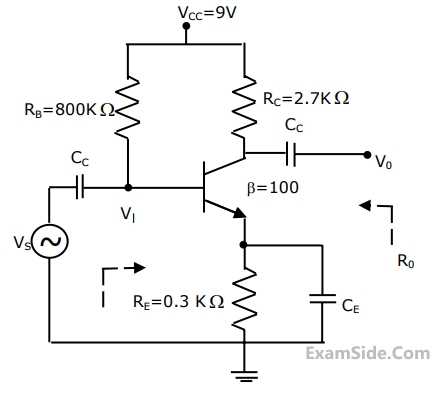
$$\beta = 100,\,{g_m} = 0.3861\,{\rm A}/V,\,{r_0} = \infty ,\,{r_\pi } = 259\,\Omega, $$
$${R_s} = 1\,K\Omega ,{R_B} = 93\,K\Omega ,\,{R_C} = 250\,\Omega, $$
$${R_L} = 1\,K\Omega ,\,{C_1} = \infty \,\,and\,\,{C_2} = 4.7\,\mu F.$$

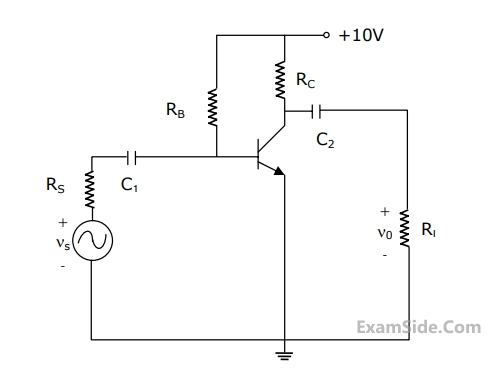
The Resistance seen by the source Vs is

Consider the common emitter amplifier shown below with the following circuit parameters:

$$\beta = 100,\,{g_m} = 0.3861\,{\rm A}/V,\,{r_0} = \infty ,\,{r_\pi } = 259\,\Omega, $$
$${R_s} = 1\,K\Omega ,{R_B} = 93\,K\Omega ,\,{R_C} = 250\,\Omega, $$
$${R_L} = 1\,K\Omega ,\,{C_1} = \infty \,\,and\,\,{C_2} = 4.7\,\mu F.$$

The lower cut-off frequency due to C₂ is

The transfer characteristic for the precision rectifier circuit shown below is (assume ideal OP-AMP and practical diodes)

Assuming the OP-AMP to be ideal, the voltage gain of the amplifier shown below is

Consider a base band binary PAM receiver shown below. The additive channel noise $$n(t)$$ is white with power spectral density $${S_N}\left( f \right) = {N_0}/2 = {10^{ - 20}}$$ $$W/Hz$$. The low-pass filter is ideal with unity gain and cut -off frequency $$1MHz$$. Let $${Y_k}$$ represent the random variable $$y\left( {{t_k}} \right)$$.
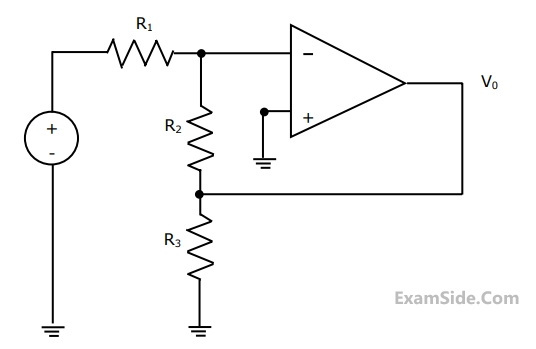
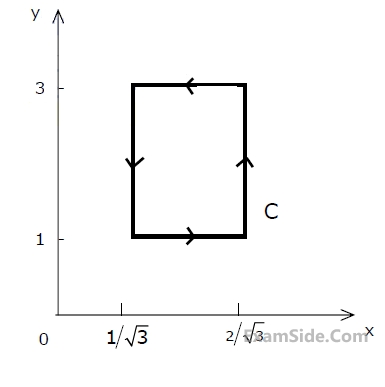
$${Y_k} = {N_k}$$ if transmitted bit $${b_k} = 0$$
$${Y_k} = a + {N_k}$$ if transmitted bit $${b_k} = 1$$
Where $${b_k} = 0$$ represents the noise sample value. The noise sample has a probability density function, $${P_{{N_k}}}\left( n \right)\,\,\,\,\,\,\, = 0.5\alpha {e^{ - \alpha \left| n \right|}}$$ (This has mean zero and variance $$2/{\alpha ^2}$$). Assume transmitted bits to be equiprobable and threshold $$z$$ is set to $$a/2 = {10^{ - 6}}V$$.

The value of the parameter $$\alpha $$( in V^-1 ) is

Consider the pulse shape s(t) as shown. The impulse response h(t) of the filter matched to this pulse is

X(t) is a stationary process with the power spectral density S_x(f) > 0 for all f. The process is passed through a system shown below.

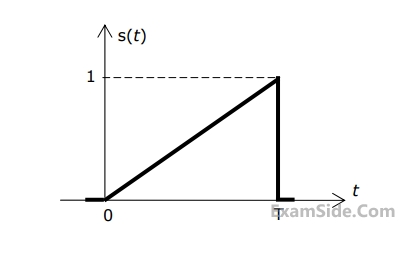
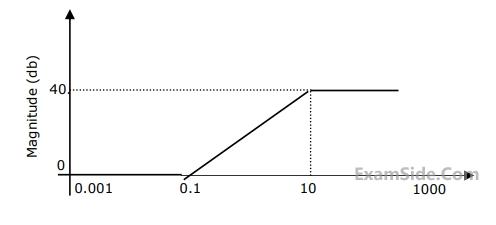
Let S_y(f) be the power spectral density of Y(t). Which one of the following statements is correct?

Consider a base band binary PAM receiver shown below. The additive channel noise $$n(t)$$ is white with power spectral density $${S_N}\left( f \right) = {N_0}/2 = {10^{ - 20}}$$ $$W/Hz$$. The low-pass filter is ideal with unity gain and cut -off frequency $$1MHz$$. Let $${Y_k}$$ represent the random variable $$y\left( {{t_k}} \right)$$.
$${Y_k} = {N_k}$$ if transmitted bit $${b_k} = 0$$
$${Y_k} = a + {N_k}$$ if transmitted bit $${b_k} = 1$$
Where $${b_k} = 0$$ represents the noise sample value. The noise sample has a probability density function, $${P_{{N_k}}}\left( n \right)\,\,\,\,\,\,\, = 0.5\alpha {e^{ - \alpha \left| n \right|}}$$ (This has mean zero and variance $$2/{\alpha ^2}$$). Assume transmitted bits to be equiprobable and threshold $$z$$ is set to $$a/2 = {10^{ - 6}}V$$.

The probability of bit error is

Consider an angle modulated signal x(t) = 6cos[2$$\mathrm\pi$$x10⁶ t+2sin(8000$$\mathrm\pi$$t) + 4cos(8000$$\mathrm\pi$$t)] V. The average power of x(t) is.

The transfer function Y(s)/R(s) of the system shown is

A system with the transfer function $${{Y(s)} \over {X(s)}} = {s \over {s + p}},$$ has an output y(t)=$$\cos \left( {2t - {\pi \over 3}} \right),$$ for input signal x(t)=$$p\cos \left( {2t - {\pi \over 2}} \right).$$ Then the system parameter 'p' is

For the asymptotic Bode magnitude plot shown below, the system transfer function can be

A unity negative feedback closed loop system has a plant with the transfer function $$G(s) = {1 \over {{s^2} + 2s + 2}}$$ and a controller $${G_c}(s)$$ in the feed forward path. For a unit set input, the transfer function of the controller that gives minimum steady sate error is

The signal flow graph of a system is shown below.

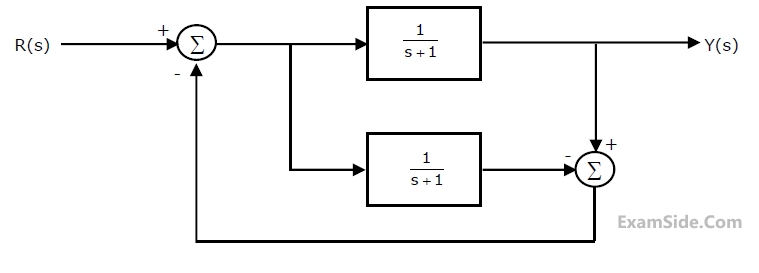
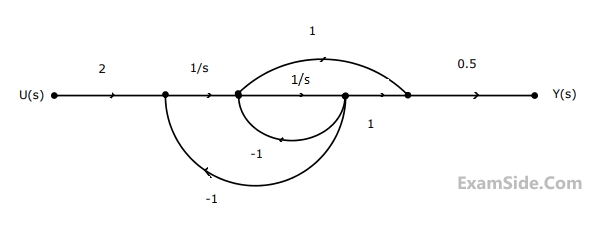
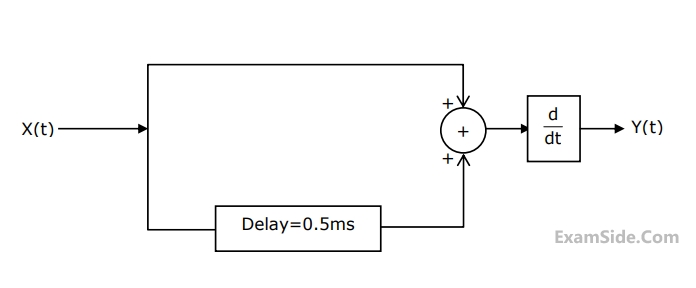
The state variable representation of the system can be

The signal flow graph of a system is shown below.

The transfer function of the system is

Assuming that all flip-flops are in reset condition initially, the count sequence observed at Q_A in the circuit shown is

The Boolean function realized by the logic circuit shown is

For the output F to be 1 in the logic circuit shown, the input combination should be

Match the logic gates in column A with their equivalents in column B.

A transmission line has a characteristic impedance of 50 $$\Omega $$ and a resistance of 0.1 $$\Omega $$/m. If the line is distortionless, the attenuation constant (in Np/m) is

If the scattering matrix [S] of a two port network is $$$\left[ S \right] = \left[ {\matrix{ {0.2\,\angle \,\,{0^ \circ }} & {0.9\,\,\angle \,\,{{90}^ \circ }} \cr {0.9\,\angle \,\,{{90}^ \circ }} & {0.1\,\angle \,{{90}^ \circ }} \cr } } \right]$$$ then the network is

In the circuit shown, all the transmission line sections are lossless. The Voltage Standing Wave Ration (VSWR) on the 60W line is

A plane wave having the electric field component $$${\overrightarrow E _i} = 24\,\,\cos \,\,\left( {3 \times {{10}^8}\,t - \beta \,y} \right){\widehat a_z}\,\,V/m$$$
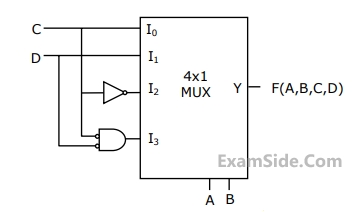
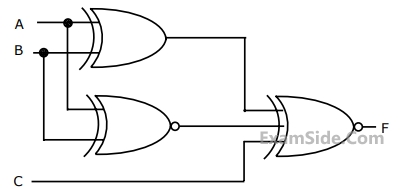
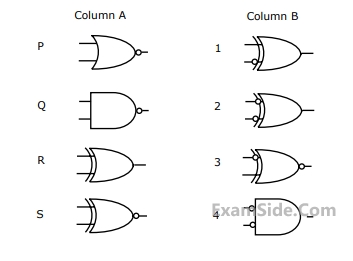
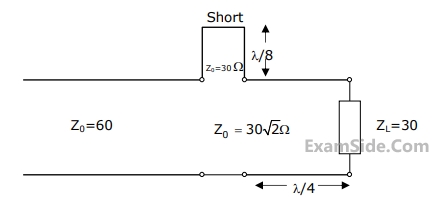
and traveling in free space is incident normally on a lossless medium with $$\mu = {\mu _0}$$ and $$\varepsilon = 9\,\,{\varepsilon _0},$$ which occupies the region $$y \ge 0.$$ The reflected magnetic field component is given by

If $$\overrightarrow{\mathrm A}\;=\;\mathrm{xy}\;{\widehat{\mathrm a}}_\mathrm x\;+\;\mathrm x^2\;{\widehat{\mathrm a}}_\mathrm y$$ then $$\oint\overrightarrow{\mathrm A}.\overrightarrow{\mathrm d}\mathcal l$$ over the path shown in the figure is

The silicon sample with unit cross-sectional area shown below is in thermal equilibrium. The following information is given: T=300K, electronic charge=1.6x10^{- 19}C, thermal voltage=26mV and electron mobility = 1350cm²/V-s

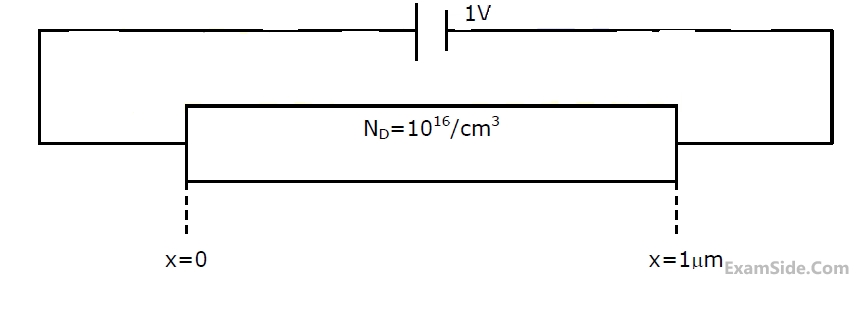
The magnitude of the electric field at x=0.5 μm is

The silicon sample with unit cross-sectional area shown below is in thermal equilibrium. The following information is given: T=300K, electronic charge=1.6x10^{- 19}C, thermal voltage=26mV and electron mobility = 1350cm²/V-s

The magnitude of the electron drift current density at x=0.5 μm is

In a uniformly doped BJT, assume that N_E, N_B and N_C are the emitter, base and collector dopings in atoms/cm³, respectively. If the emitter injection efficiency of the BJT is close unity, which one of the following conditions is TRUE?

The eigen values of a skew-symmetric matrix are

If $$\,{e^y} = {x^{1/x}}\,\,$$ then $$y$$ has a

If $$\overrightarrow A = xy\,\widehat a{}_x + {x^2}\widehat a{}_y\,\,$$ then $$\,\,\oint {\overrightarrow A .d\overrightarrow r \,\,} $$ over the path shown in the figure is

A fair coin is tossed independently four times. The probability of the event ''The number of times heads show up is more than the number of times tails show up'' is

A function $$n(x)$$ satisfies the differential equation $${{{d^2}n\left( x \right)} \over {d{x^2}}} - {{n\left( x \right)} \over {{L^2}}} = 0$$ where $$L$$ is a constant. The boundary conditions are $$n(0)=k$$ and $$n\left( \propto \right) = 0.$$ The solution to this equation is

Consider a differential equation $${{dy\left( x \right)} \over {dx}} - y\left( x \right) = x\,\,$$ with initial condition $$y(0)=0.$$ Using Euler's first order method with a step size of $$0.1$$ then the value of $$y$$ $$(0.3)$$ is

The residues of a complex function $$X\left( z \right) = {{1 - 2z} \over {z\left( {z - 1} \right)\left( {z - 2} \right)}}$$ at it poles

For the 8085 assembly language program given below, the content of the accumulator after the executions of the program is
3000 MVI A, 45H
3002 MOV B, A
3003 STC
3004 CMC
3005 RAR
3006 XRA B

In the circuit shown, the device connected to Y5 can have address in the range

In the circuit shown, the device connected to Y₅ can have address in the range

For parallel RLC circuit, which one of the following statements is NOT correct?

The current I in the circuit shown is

For the two-port network shown below, the short-circuit admittance parameter matrix is

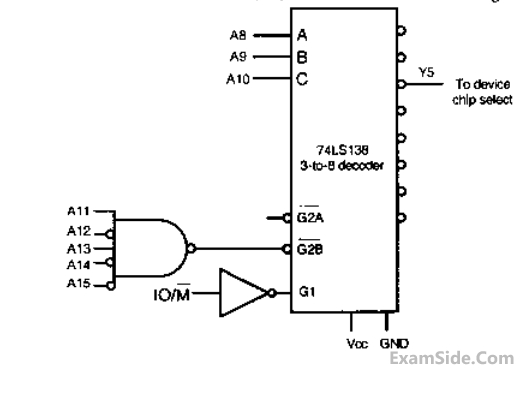
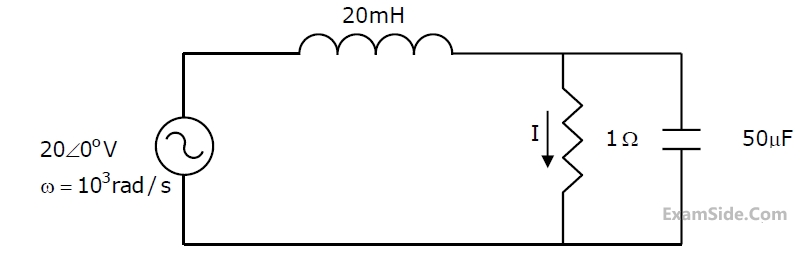
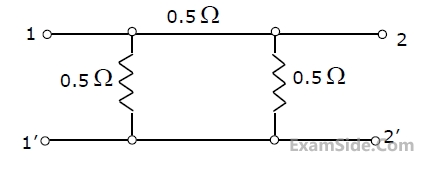
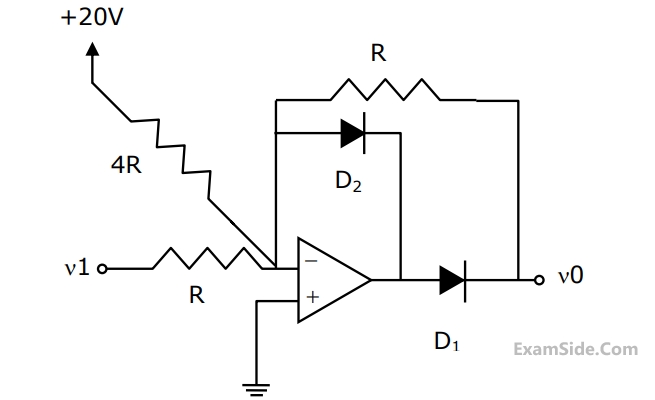
In the circuit shown, the power supplied by the voltage source is

In the circuit shown, the switch S is open for a long time and is closed at t=0. The current i(t) for t ≥ 0⁺ is

Two discrete time systems with impulse responses $${h_1}\left[ n \right]\, = \delta \left[ {n - 1} \right]$$ and $${h_2}\left[ n \right]\, = \delta \left[ {n - 2} \right]$$ are connected in cascade. The overall impulse response of the cascaded system is

Consider an angle modutated signal $$x(t) = 6\,\,\cos \,[2\,\pi \, \times {10^6}t + 2\sin (8000\pi t)\,4\cos (8000\pi t)]$$ V.

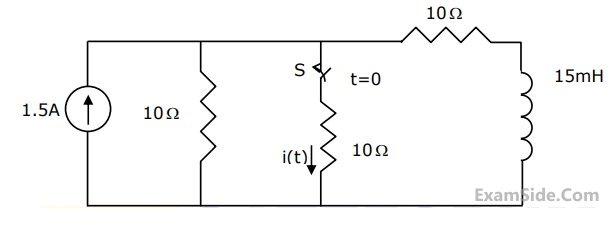
The average power of x(t) is

The Nyquist sampling rate for the signal $$s(t) = {{\sin \,(500\pi t)} \over {\pi \,t}} \times {{\sin \,(700\pi t)} \over {\pi \,t}}$$ is given by

A system with the transfer function $${{Y(s)} \over {X(s)}} = {s \over {s + p}}\,\,$$ has an output
$$y(t) = \cos \left( {2t - {\pi \over 3}} \right)\,$$ for the input signal
$$x(t) = p\cos \left( {2t - {\pi \over 2}} \right)$$. Then, the system parameter 'p' is

Consider the pulse shape s(t) as shown. The impulse response h(t) of the filter matched to this pulse is

The transfer function of a discrete time LTI system is given by
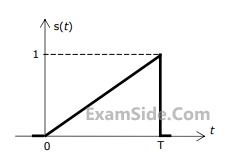
$$H\left( z \right) = {{2 - {3 \over 4}{z^{ - 1}}} \over {1 - {3 \over 4}{z^{ - 1}} + {1 \over 8}{z^{ - 2}}}}$$

Consider the following statements:
S1: The system is stable and causal for $$ROC:\,\,\,\left| z \right| > \,1/2$$
S2: The system is stable but not causal for $$ROC:\,\,\,\left| z \right| < \,1/4$$
S3: The system is neither stable nor causal for $$ROC:\,\,1/4\, < \,\left| z \right| < \,{\raise0.5ex\hbox{$\scriptstyle 1$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 2$}}$$

Which one of the following statements is valid?

A continuous time LTI system is described by $${{{d^2}y(t)} \over {d{t^2}}} + 4{{dy(t)} \over {dt}} + 3y(t)\, = 2{{dx(t)} \over {dt}} + 4x(t)$$.

Assuming zero initial conditions, the response y(t) of the above system for the input x(t) = $${e^{ - 2t}}$$ u(t) is given by

Consider the z-transform
X(z)=5$${z^2} + 4{z^{ - 1}} + 3;0 < \left| z \right| < \infty $$.

The inverse z - transform x$$\,\left[ n \right]$$ is

For an N-point FFT algorithm with N = $${2^m}$$ which one of the following statements is TRUE?

Given f(t) = $${L^{ - 1}}\left[ {{{3s + 1} \over {{s^3} + 4{s^2} + \left( {K - 3} \right)s}}} \right].$$ If $$\matrix{ {Lim\,f\,\left( t \right) = 1,} \cr {t \to \infty } \cr } \,\,$$ then the value of K is

The trigonometric Fourier series for the waveform f(t) shown below contains

The question below consists of a pair of related of related words followed by four pairs of words. Select the pair that best expresses the relation in the original pair.

Unemployed : Worker

Which of the following options is the closest in meaning to the world below:

Circuitous

Choose the most appropriate word from the options given below to complete the following sentence:

His rather casual remarks on politics _______ his lack of seriousness about the subject.

Choose the most appropriate word from the options given below to complete the following sentence:

If we manage to ________ our natural resources, we would leave a better planet for our children.

Modern warfare has changed from large scale clashes of armies to suppression of civilian populations. Chemical agents that do their work silently appear to be suited to such warfare; and regretfully, there exist people in military establishments who think that chemical agents are useful tools for their cause.

Which of the following statements best sums up the meaning of the above passage:

Hari (H), Gita (G), Irfan (I) and Saira (S) are siblings (i.e. brothers and sisters). All were born on 1^st January. The age difference between any two successive siblings (that is born one after another) is less than 3 years. Given the following facts:

i. Hari’s age + Gita’s age > Irfan’s age + Saira’s age.

ii. The age difference between Gita and Saira is 1 year. However, Gita is not the oldest and Saira is not the youngest.

iii. There are not twins.

In what order were they born (Oldest first)?

If 137+276=435 how much is 731+672?

25 persons are in a room. 15 of them play hockey, 17 of them play football and 10 of them play both hockey and football. Then the number of persons playing neither hockey nor football is:

5 skilled workers can build a wall in 20 days; 8 semi-skilled workers can build a wall in 25 days; 10 unskilled workers can build a wall in 30 days. If a team has 2 skilled, 6 semi-skilled and 5 unskilled workers, how long will it take to build the wall?

Given digits 2,2,3,3,3,4,4,4,4 how many distinct 4 digit numbers greater than 3000 can be formed?