GATE ECE
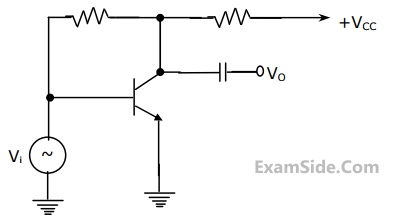
(1) less expensive transformer
(2) smaller size transformer, and
(3) suitability for higher voltage application.
Of these,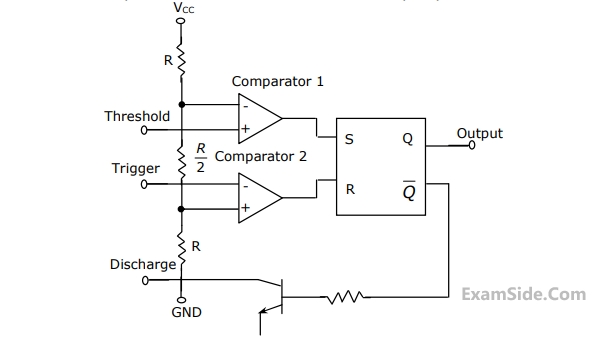
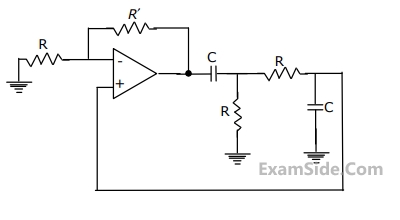
(i) Determine the range of K for the system to be stable.
(ii) Can the system be marginally stable? If so, find the required value of K and the frequency of sustained oscillation.


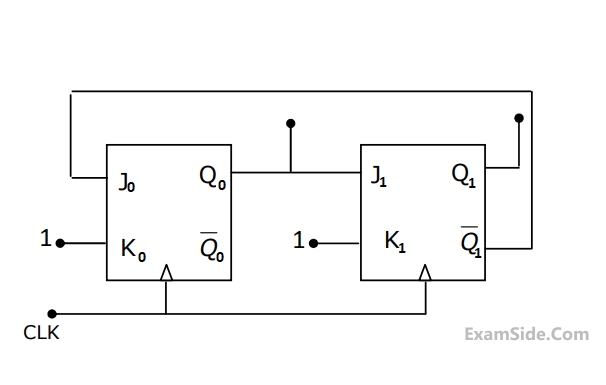
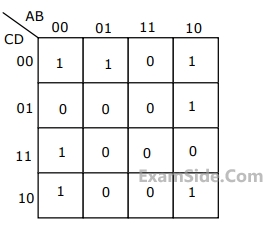
(a) Will the counter lockout if it happens to be in any one of the unused states?
(b) Find the maximum rate at which the counter will operate satisfactorily. Assume the propagation delays of flip-flop and AND gate to be tF and tA
List 1
A. Flash converter
B. Dual slope converter
C. Successive approximation Converter List 2
1. requires a conversion time of the order of a few seconds
2. requires a digital- to- analog converter
3. minimizes the effect of power supply interference.
4. requires a very complex hardware.
5. It is a tracking A/D converter.
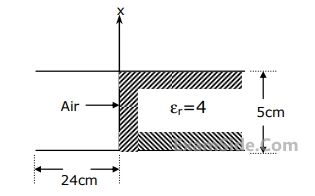
Its frequency is 10 GHz.
(i) Investigate if this wave is a plane wave.
(ii) Determine its propagation constant, and
(iii) Calculate the phase velocity in $$y$$-direction.
$$\mathop {Lim}\limits_{t \to \infty } f\left( t \right) = $$ ____________.

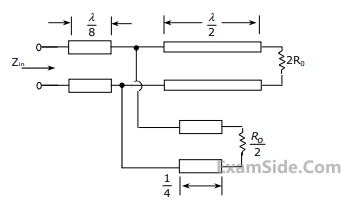
A voltage source of internal impedance $${\mathrm R}_\mathrm s\;+\;{\mathrm{jX}}_\mathrm s$$ supplies power to a load of impedance $${\mathrm R}_\mathrm L\;+\;{\mathrm{jX}}_\mathrm L$$ in which only $${\mathrm R}_\mathrm L$$ is variable. Determine the value of $${\mathrm R}_\mathrm L$$ for maximum power transfer from the source to the load. Also, find the numerical value of $${\mathrm R}_\mathrm L$$ if the source impedance is 3.0 Ω (purely resistive) and $${\mathrm X}_\mathrm L$$ is 4.0 Ω.
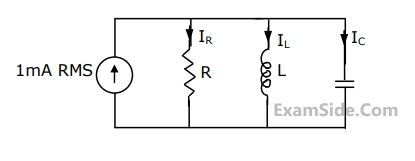
Superposition theorem is NOT applicable to networks containing
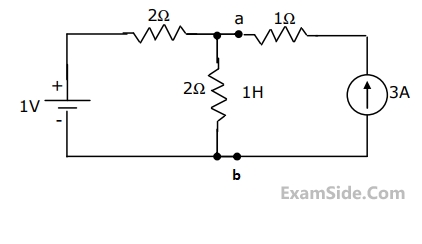
The voltage across the terminals a and b in Fig. is
The Nodal method of circuit analysis is based on