In the circuit shown, assume that diodes D₁ and D₂ are ideal. In the steady-state condition the average voltage V_ab (in Volts) across the 0.5 μF capacitor is _____.

In the circuit shown using am ideal opamp, the 3-dB cut-off frequency (in Hz) is _____.

In the circuit shown, assume that the opamp is ideal. If the gain ($${V_0}/{V_{in}}$$) is -12, the value of R (in K$$\Omega $$) is _____.

The modulation scheme commonly used for transmission from GSM mobile terminals is

A random binary wave $$y(t)$$ is given by $$$y\left( t \right) = \sum\limits_{n = - \infty }^\infty {{X_n}p\left( {t - nT - \phi } \right)} $$$

where $$p(t) = u(t) - u(t - T)$$, $$u(t)$$ is the unit step function and $$\phi $$ is an independent random variable with uniform distribution in $$[0, T]$$. The sequence $$\left\{ {{X_n}} \right\}$$ consists of independent and identically distributed binary valued random variables with $$P\left\{ {{X_n} = + 1} \right\} = P\left\{ {{X_n} = - 1} \right\} = 0.5$$ for each $$n$$.

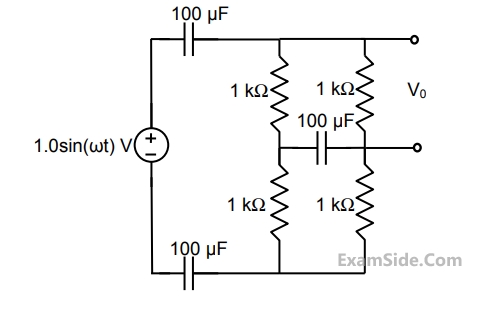
The value of the autocorrelation $${R_{yy}}\left( {{{3T} \over 4}} \right)\underline{\underline \Delta } E\left[ {y\left( t \right)y\left( {t - {{3T} \over 4}} \right)} \right]\,\,$$

equals ------------ .

Consider the Bode plot shown in the figure. Assume that all the poles and zeroes are real-valued. The value of f_H - f_L (in Hz) is ______.

The impulse response of an LTI system can be obtained by

The characteristic equation of an LTI system is given by
F(s) = s⁵ + 2s⁴ +3s³ + 6s² - 4s - 8 = 0.The number of roots that lie strictly in the left half s-plane is _____.

For the system shown in the figure, s = –2.75 lies on the root locus if K is_____.

The phase margin (in degrees) of the system G(s)=$${{10} \over {\left( {s + 10} \right)}}$$ is ___________.

The transfer function of a first-order controller is given as $${G_c}(s) = {{K\left( {s + a} \right)} \over {s + b}}$$

where k, a and b are positive real numbers. The condition for this controller to act as a phase lead compensator is

The position control of a DC servo-motor is given in the figure. The values of the parameters are
K_t=1 N-m/A, R_a=$$1\Omega ,$$ L_a=0.1H,
J=5kg-m², B=1 N-m/(rad/sec) and K_b=1V/(rad/sec).
The steady-state position response (in radians) due to unit impulse disturbance torque T_d is ____.

A network is described by the state model as $$$\eqalign{ & {\mathop x\limits^ \bullet _1} = 2{x_1} - {x_2} + 3u, \cr & \mathop {{x_2}}\limits^ \bullet = - 4{x_2} - u, \cr & y = 3{x_1} - 2{x_2} \cr} $$$

the transfer function H(s)$$\left[ { = {{Y\left( s \right)} \over {U\left( s \right)}}} \right]is$$

In the circuit shown, diodes $${D_1}$$ ,$${D_2}$$ and $${D_3}$$ are ideal, and the inputs $${E_1}$$ , $${E_2}$$ and $${E_3}$$ are “0 V” for logic ‘0’ and “10 V” for logic ‘1’. What logic gate does the circuit represent?

A universal logic gate can implement any Boolean function by connecting sufficient number of them appropriately. Three gates are shown.

Which one of the following statesments is TRUE?

The circuit shown consists of J-K flip-flops, each with an active low asynchronous reset ($$\overline {{R_d}} $$ input). The counter corresponding to this circuit is

A three bit pseudo random number generator is shown. Initially the value of output Y = Y₂ Y₁ Y₀ is set to 111. The value of output Y after three clock cycles is

An SR latch is implemented using TTL gates as shown in the figure. The set and reset pulse inputs are provided using the push-button switches. It is observed that the circuit fails to work as desired. The SR latch can be made functional by changing

A 200 m long transmission line having parameters shown in the figure is terminated into a load ܴ$$R_L$$. The line is connected to a 400 V source having source resistance $$R_S$$ through a switch, which is closed at t = 0. The transient response of the circuit at the input of the line (z = 0) is also drawn in the figure. The value of ܴ$$R_L$$ (in $$\Omega $$ ) is ___________.

A coaxial cable is made of two brass conductors. The spacing between the conductors is filled with Teflon $$\left( {{\varepsilon _r} = 2.1,\,\,\tan \,\,\delta = \,0} \right)$$. Which one of the following circuits can represent the lumped element model of a small piece of this cable having length $$\Delta \,\,z\,\,?$$

Consider the 3 m long lossless air-filled transmission line shown in the figure. It has a characteristic impedance of $$120\pi \,\Omega $$, is terminated by a short circuit, and is excited with a frequency of 37.5 MHz. What is the nature of the input impedance $$({Z_{in}})$$?

The directivity of an antenna array can be increased by adding more antenna elements, as a larger number of elements

A coaxial capacitor of inner radius 1 mm and outer radius 5 mm has a capacitance per unit length of 172 pF/m. If the ratio of outer radius to inner is doubled, the capacitance per unit length (in pF/m) is _____.

The electric field profile in the depletion region of a p-n junction in equilibrium is shown in the figure. Which one of the following statements is NOT TRUE?

In the circuit shown in the figure, the BJT has a current gain (β) of 50. For an emitter-base voltage V_EB = 600 mV, the emitter-collector voltage V_EC(in Volts) is ______.

If the base width in a bipolar junction transistor is doubled, which one of the following statements will be TRUE?

An npn BJT having reverse saturation current $$I_s\;=\;10^{-15}\;A$$ is biased in the forward active region with V_BE = 700 mV. The thermal voltage (V_T) is 25 mV and the current gain (β) may vary from 50 to 150 due to manufacturing variations. The maximum emitter current (in μA) is _____.

Which one of the following processes is preferred to from the gate dielectric (SiO₂) of MOSFETs?

In the circuit shown, both the enhancement mode NMOS transistors have the following characteristics: k_n = $${\mu _n}{C_{ox}}(W/L) = 1m{\rm A}/{V^2}$$ ; V_TN = 1V. Asuume that the channel length modulation parameter $$\lambda $$ is zero and body is shorted to source. The minimum supply voltage V_DD (in volts) needed to ensure that transistor M₁ operates in saturation mode of operation is _____

The current in an enhancement mode NMOS transistor biased in saturation mode was measured to be 1 mA at a drain-source voltage of 5 V. When the drain-source voltage was increased to 6 V while keeping gate-source voltage same, the drain current increased to 1.02 mA. Assume that drain to source saturation voltage is much smaller than the applied drain-source voltage. The channel length modulation p[arameter $$\lambda $$ (in V^-1) is _______

For $$A = \left[ {\matrix{ 1 & {\tan x} \cr { - \tan x} & 1 \cr } } \right],$$ the determinant of $${A^T}\,{A^{ - 1}}$$ is

The value of $$\sum\limits_{n = 0}^\infty {n{{\left( {{1 \over 2}} \right)}^n}\,\,} $$ is _______.

The contour on the $$x-y$$ plane, where the partial derivative of $${x^2} + {y^2}$$ with respect to $$y$$ is equal to the partial derivative of $$6y+4x$$ with respect to $$'x',$$ is

A fair die with faces $$\left\{ {1,2,3,4,5,6} \right\}$$ is thrown repeatedly till $$'3'$$ is observed for the first time. Let $$X$$ denote the number of times the dice is thrown. The expected value of $$X$$ is _________.

The variance of the random variable $$X$$ with probability density function $$\,f\left( x \right) = {1 \over 2}\left| x \right|{e^{ - \left| x \right|}}\,\,$$ is ___________.

Consider the differential equation $${{{d^2}x\left( t \right)} \over {d{t^2}}} + 3{{dx\left( t \right)} \over {dt}} + 2x\left( t \right) = 0$$
Given $$x(0) = 20$$ & $$\,x\left( 1 \right) = {{10} \over e},$$ where $$e=2.718,$$

The value of $$x(2)$$ is

The Newton-Raphson method is used to solve the equation $$f\left( x \right) = {x^3} - 5{x^2} + 6x - 8 = 0.$$ Taking the initial guess as $$x=5$$, the solution obtained at the end of the first iteration is ________.

If $$C$$ is a circle of radius $$r$$ with centre $${z_0}$$ in the complex $$z$$-plane and if $$'n'$$ is a non-zero integer, then $$\oint\limits_c {{{dz} \over {{{\left( {z - {z_0}} \right)}^{n + 1}}}}} $$ equals

Consider the function $$g\left( t \right) = {e^{ - t}}\,\sin \left( {2\pi t} \right)u\left( t \right)$$ ,where $$u(t)$$ is the unit step function. The area under $$g(t)$$ is _______________.

Which one of the following 8085 microprocessor programs correctly calculates the product of two 8-bit numbers stored in registers B and C?

At very high frequencies, the peak output voltage V₀ (in Volts) is ______.

In the circuit shown, the current $${\rm I}$$ flowing through the $$50\,\Omega $$ resistor will be zero if the value of capacitor C (in $$\mu F$$) is ________ .

The ABCD parameters of the following 2-port network are

In the circuit shown, the voltage V_x (in Volts) is ______.

For the circuit shown in the figure, the Thevenin equivalent voltage (in Volts) across terminals a-b is _____.

Let $$\widetilde x\left[ n \right]\, = \,1 + \cos \left[ {{{\pi n} \over 8}} \right]$$ be a periodic signal with period 16. Its DFS coefficients are defined by
$${a_k}$$ = $${1 \over {16}}\sum\limits_{n = 0}^{15} {\widetilde x} \left[ n \right]\exp \left( { - j{\pi \over 8}kn} \right)$$ for all k. The value of the coeffcients $${a_{31}}$$ is _____________________.

A realization of a stable discrete time system is shown in the figure. If the system is excited by a unit step sequence input x[n ] , the response y[ n] is

Suppose x $$\left[ n \right]$$ is an absolutely summable discrete-time signal. Its z-transform is a rational function with two poles and two zeroes. The poles are at z = ± 2j. Which one of the following statements is TRUE for the signal x=$$\left[ n \right]$$ ?

The impulse response of an LTI system can be obtained by

The complex envelope of the bandpass signal $$x(t)\, = \, - \sqrt 2 \left( {{{\sin (\pi t/5)} \over {\pi t/5}}} \right)\sin \left( {\pi t - {\pi \over 4}} \right),$$ centered about f = $${1 \over {2\,}}\,Hz,$$ is

Two sequence $${x_1}\left[ n \right]$$ and $${x_2}\left[ n \right]$$ have the same energy.
Suppose $${x_1}\left[ n \right]$$ $$ = \alpha \,{0.5^n}\,u\left[ n \right],$$ where $$\alpha $$ is a positive real number and $$u\left[ n \right]\,$$ is the unit step sequence. Assume $$${x_2}\left[ n \right] = \,\left\{ {\matrix{ {\sqrt {1.5} } & {for\,\,\,n = 0,1} \cr 0 & {otherwise} \cr } } \right.$$$

Then the value of $$\,\alpha $$ is________.

Consider a four-point moving average filter defined by the equation $$y[n] = \sum\limits_{i = 0}^3 {{\alpha _i}x[n - i]} $$. The condition on the filter coefficients that results in a null at zero frequency is

Consider a continuous-time signal defined as $$x(t) = \left( {{{\sin \,(\pi t/2)} \over {(\pi t/2)}}} \right)*\sum\limits_{n = - \infty }^\infty {\delta (t - 10n)} $$ Where ' * ' denotes the convolution operation and t is in seconds. The Nyquist sampling rate (in samples/sec) for x(t) is __________________.

Consider the function $$g(t) = {e^{ - t}}\,\,\,\sin (2\pi t)\,u(t)$$ where u(t) is the unit step function. The area under g(t) is_______________.

The complex envelope of the bandpass signal $$x(t) = - \sqrt 2 \left( {{{\sin \,(\pi t/5)} \over {\pi t/5}}} \right)\,\sin \,\left( {\pi t - {\pi \over 5}} \right)$$, centered about $$\,f = {1 \over 2}\,\,Hz$$, is

The value of $$\sum\limits_{n = 0}^\infty n {\left( {{1 \over 2}} \right)^n}$$ is ________________.

Find the missing sequence in the letter series below:
A, CD, GHI, ? , UVWXY

If x>y>1, which of the following must be true? $$$\begin{array}{l}\mathrm i.\;\ln\left(\mathrm x\right)>\ln\left(\mathrm y\right)\;\;\;\;\;\;\;\;\;\;\mathrm{ii}.\;\;\mathrm e^\mathrm x>\mathrm e^\mathrm y\\\mathrm{iii}.\;\mathrm y^\mathrm x>\mathrm x^\mathrm y\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathrm{iv}.\;\cos\left(\mathrm x\right)>\cos\left(\mathrm y\right)\end{array}$$$