GATE ECE
If the signal to quantization noise ratio required in uniformly quantizing the signals is 43.5 dB, the step size of the quantization is approximately
If the positive values of the signal are uniformly quantized with a step size of 0.05 V, and the negative values are uniformly quantized with a step size of 0.1V, the resulting signal to quantization noise ratio is approximately
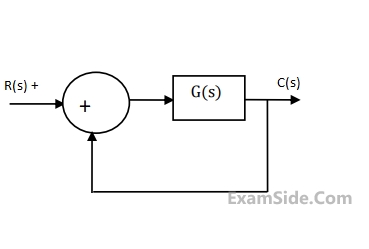
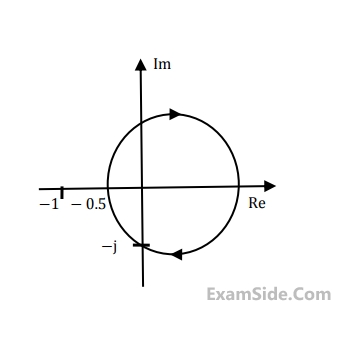 The gain and phase margins of G(s) for closed loop stability are
The gain and phase margins of G(s) for closed loop stability are 
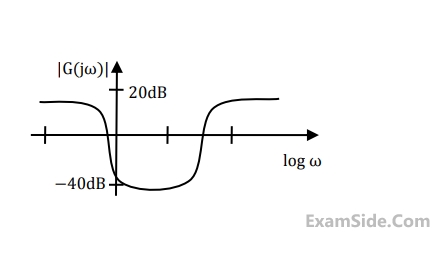
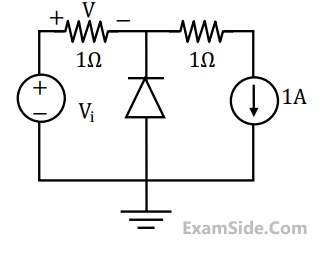
 Which of the foloowing statements is true?
Which of the foloowing statements is true?
where p and q are arbitrary real numbers. Which of the following statesments about the controllability of the system is true?



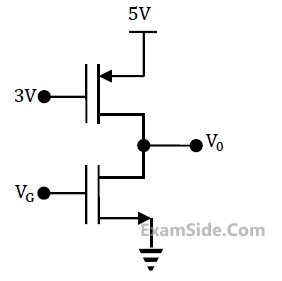
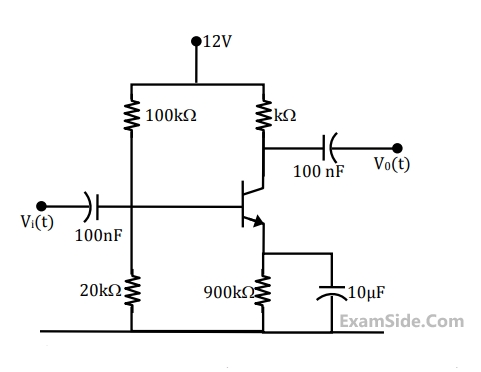
For small increase in VG beyond 1 V, which of the following gives the correct description of the region of operation of each MOSFET?

Estimate the output voltage V0 for VG =1.5 V. [Hints: Use the appropriate current-voltage equation for each MOSFET, based on the answer]
Note: $$C$$ and $${S_C}$$ refer to any closed contour and any surface whose boundary is $$C.$$

Group $$I$$
$$P:$$$$\,\,\,$$ $${{dy} \over {dx}} = {y \over x}$$
$$Q:$$$$\,\,\,$$ $${{dy} \over {dx}} = {{ - y} \over x}$$
$$R:$$$$\,\,\,$$ $${{dy} \over {dx}} = {x \over y}$$
$$S:$$$$\,\,\,$$ $${{dy} \over {dx}} = {{ - x} \over y}$$
Group $$II$$
$$(1)$$$$\,\,\,$$ Circle
$$(2)$$$$\,\,\,$$ straight lines
$$(3)$$$$\,\,\,$$ Hyperbola
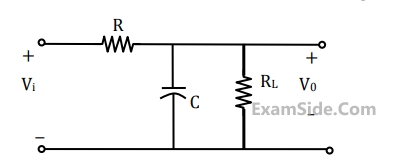
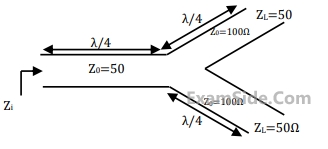
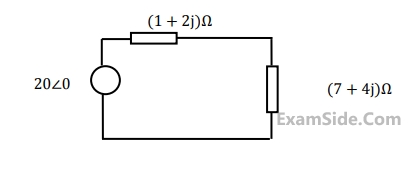
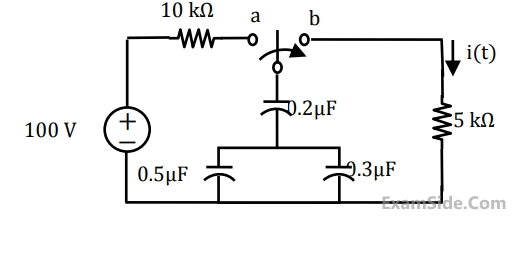
The value of the load resistance $${R_L}$$ is
A fully charged mobile phone with a 12 V battery is good for a 10 minute talk-time. Assume that, during the talk-time, the battery delivers a constant current of 2 A and its voltage drops linearly from 12 V to 10 V as shown in the figure. How much energy does the battery deliver during this talk-time?

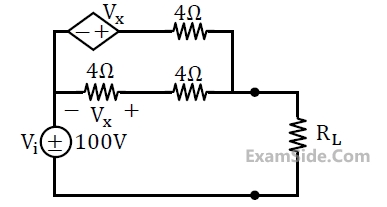
In the interconnection of ideal sources shown in the figure, it is known that the 60V source is absorbing power.

Which of the following can be the value of the current source I?
Where h(t) is shown in the graph.
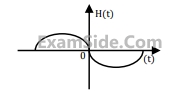
Which of the following four properties are possessed by the system?
BIBO: Bounded input gives a bounded output.
Causal: The system is casual.
LP: The system is low pass.
LTI: The system is linear and time- invariant.
S1: H(z) is a low-pass filter.
S2: H(z) is an FIR filter.
Which of the following is correct?
x(n)= $${\left( {{1 \over 3}} \right)^{n}}u(n) - {\left( {{1 \over 2}} \right)^{ n}}\,u( - n - 1)$$ is
P. Cosine terms if it is even
Q. Sine terms if it is even
R. Cosine terms if it odd
S. Sine terms if it is odd
Which of the above statement are correct?