The transistor in the circuit shown in the figure. is so biased (dc biasing N/W is not shown) that the dc collector current I_C = 1mA. Supply is V_CC = 5V.

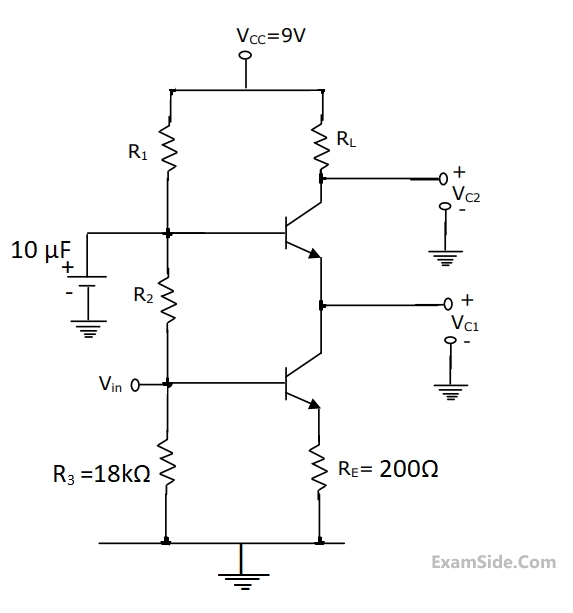
The N/W components have following values, R_C = 2$$k\Omega $$,
R_S = $$1.4k\Omega $$,
R_E = $$100\Omega $$.

The transistor has specifications, $$\beta \,\, = \,\,100$$
and base spreading resistance $${r_{bb\,}}^1\, = \,100\Omega $$

$$Assume\,\,{{KT} \over q}\,\, = \,\,25\,mV$$

Evaluate input resistance R_i for two cases. At a frequency of 10 kHz

(a)C_E, the bypass capacitor across R_E is 25 $$\mu F$$
(b)The bypass capacitor C_E is removed leaving R_E unbypassed.

In the cascade amplifier circuit shown below, determine the values of R₁, R₂ and R_L. Such that the quiescent current through the transistors is 1mA and the collector voltage V_c1 = 3V, and V_c2 = 6V. Tke V_BE = 0.7V, Transistor $$\beta $$ to be hifgh and base currents to be negligible.

An Amplifier a has 6 dB gain and 50 $$\Omega $$ input and output impedances. The noise figure of this Amplifier as shown in the figure is 3 dB. A cascade of two such Amplifiers as in the figure will have a noise figure of

Negative feedback in

1. Voltage series configuration
2.Current shunt configuration

(a) increases input impedance
(b) decreases input impedance
(c) increases closed loop gain
(d) leads to ascillation.

An IC 555 chip has been used to construct a pulse generator. Typical pin connections with components is shown below in fig. for such application. However it is desired to generate a square pulse of 10KHz.. Evaluate values of $${R_{A\,}}$$ and $${R_{B\,}}$$ and if the capacitor has the value of 0.01$$\mu $$F for the configuration closed. If necessary you can suggest modifications in the external circuit configuration.

The output voltage V₀ of the circuit shown in the figure is

Consider the circuit given in fig. using an ideal operational Amplifier.

The characteristics of the diode are given by the relation I = I_s $$\left[ {{e^{{{qV} \over {KT}}}} - 1} \right],$$

Where V is the forward voltage across the diode
(a)Express V₀ as a function of V_i assuming V_i> 0.
(b)If R = 100K$$\Omega $$ , I_s = 1$$\mu $$A and $${{KT} \over q}\,\, = \,\,25mV$$

The line code that has zero dc component for pulse transmission of random binary data is

A deterministic signal has the power spectrum given in figure. The minimum sampling rate needed to completely represent this signal is

A probability density function is given by $$p(x) = \,K\,\,\exp \,\,( - \,{x^2}/2),\,\, - \,\infty \, < \,x < \,\infty $$.

The value of K should be

A certain linear time invariant system has the state and the output equations given below $$$\left[ {\matrix{ {\mathop {{x_1}}\limits^ \bullet } \cr {\mathop {{x_2}}\limits^ \bullet } \cr } } \right] = \left[ {\matrix{ 1 & { - 1} \cr 0 & 1 \cr } } \right]\left[ {\matrix{ {{x_1}} \cr {{x_2}} \cr } } \right] + \left[ {\matrix{ 0 \cr 1 \cr } } \right]u$$$ $$$y = \left[ {\matrix{ 1 & 1 \cr } } \right]\left[ {\matrix{ {{x_1}} \cr {{x_2}} \cr } } \right], if$$$ $${x_1}\left( 0 \right) =1 ,{x_2}\left( 0 \right) = - 1,$$ $$u\left( 0 \right) = 0,$$ then $${{dy} \over {dt}}{|_{t = 0}}$$ is

In the signal flow graph of Fig. y/x equals

Following fig. shows the block diagram representation of control system. The system in block A has an impulse response h(t ) = e^−t u(t ). The system in block B has an impulse response h(t ) = e^−2t u(t ). The block 'K' amplifies its inputs by a factor k. For the overall system with input x(t) and output y(t). (a) Find the transfer function $$\frac{y\left(s\right)}{x\left(s\right)}$$ when k =1.
(b) Find the impulse response when k = 0.
(c) Find the values of k for which the system becomes unstable.

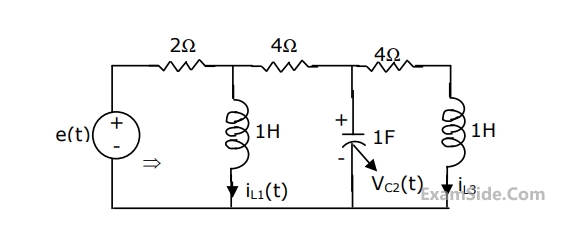
For the circuit shown in the figure, choose state variables as $${x_{1,}}{x_{2,}}{x_3}$$ to be $${i_{L1}}\left( t \right),{v_{c2}}\left( t \right),{i_{L3}}\left( t \right)$$

Wriote the state equations

$$$\left[ {\matrix{ {\mathop {{x_1}}\limits^ \bullet } \cr {\mathop {{x_2}}\limits^ \bullet } \cr {\mathop {{x_3}}\limits^ \bullet } \cr } } \right] = A\left[ {\matrix{ {{x_1}} \cr {{x_2}} \cr {{x_3}} \cr } } \right] + B\left[ {e\left( t \right)} \right]$$$

For the NMOS logic gate shown in figure, the logic function implemented is

The gate delay of an NMOS inverter is dominated by charge time rather than discharge time because

A sequence generator is shown in figure. The counter status (Q₀ Q₁ Q₃) is intialized to 010 using preset/clear inputs.
The Clock has a period of 50ns and transitions take place at the rising clock edge.
(a) Give the sequence generated at Q₀ till it repeats.
(b) What is the repetition rate for the generated sequence?

The inverter 74AL SO4 has the following specifications:
$${I_{OH}}{\,_{\max \,}} = \, - $$ 0.4mA, $${I_{OL}}$$ max = 8mA, $${I_{IH}}$$ max = $$\mu $$A , $${I_{IL\,}}_{\max \,}$$=0.1mA. The fan out based on the above will be

A signed integer has been stored in a byte using the 2's complement format. We wish to store the same integer in a 16-bit word. We should

The output of the logic gate in figure is

A 2-bit binary multiplier can be implemented using

In a J_K flip-flop, we have J=$$\overline Q $$ and K=1 (see figure). Assuming the flip-flop was intially cleared and then clocked for 6 pulses, the sequence at the Q output will be

In standard TTL the 'totem pole' stage refers to

A transmission line of 50$$\Omega $$ characteristic impedance is terminated with a 100 $$\Omega $$ resistance. The minimum impedance measured on the line is equal to

A $${\lambda \over 2}$$ section of a 600 $$\Omega $$ transmission line, short ciruited at one end and open circuited at the other end, is shown in Fig. A 100 V / 75 $$\Omega $$ generator is connected at the mid point of the section as shown in the Fig. Find the voltage at the open-ciruited end of the line.

A uniform plane wave is normally incident from air on an infinitely thick magnetic material with relative permeability 100 and relative permittivity 4 (sec in Fig.). The wave has an electric field of 1 V/meter (rms). Find the average Poynting vector inside the material.

A rectangular air-filled waveguide has a cross section of $$4\,cm\,\, \times \,\,10cm$$. The minimum frequency which can propagate in the waveguide is

A parabolic dish antenna has a conical beam 2⁰ wide. The directivity of the antenna is approximately

A dipole antenna has a sin$$\theta $$ radiation pattern where the angle $$\theta $$ is measured from the axis of the dipole. The dipole is vertically located above an ideal ground plane (Fig.). What should be the height of the dipole H in terms of wave length so as to get a null in the radiation pattern at an angle of 45⁰ from the ground plane? Find the direction of maximum radiation also.

The units of $$\frac q{KT}$$ are

The curve given by the equation $${x^2} + {y^2} = 3axy$$ is

The laplace transform of $${e^{\alpha t}}\,\cos \,\alpha \,t$$ is equal to ____________.

The decoding circuit shown below has been used to generate the active low chip select signal for a microprocessor peripheral. (The address lines are designated as $${A_0}$$ to $${A_7}$$ for I-O address)

The following instructions have been executed by an 8085 $$\mu $$P
From which address will be text instruction be fetched?

In an 8085$$\mu$$P system, the RST instruction will cause an interrupt

In the circuit of Fig., all currents and voltage are sinusoids of frequency $$\omega $$ rad/sec.

(a) Find the impedance to the right of $$\left( {A,\,\,\,\,\,\,B} \right)$$ at $$\omega \,\,\, = \,\,\,\,0$$ rad/sec and $$\omega \,\,\, = \,\,\,\,\infty $$ rad/sec.

(b) If $$\omega \,\,\, = \,\,\,\,{\omega _0}$$ rad/sec and $${i_1}\left( t \right) = \,\,{\rm I}\,\,\,\sin \,\left( {{\omega _0}t} \right)\,{\rm A},$$ where $${\rm I}$$ is positive, $${{\omega _0}\,\, \ne \,\,0}$$, $${{\omega _0}\,\, \ne \,\,\infty }$$, then find $${\rm I}$$, $${{\omega _0}}$$ and $${i_2}\left( t \right)$$

In the circuil of Fig. the equivalent impedance seen across terminals A. B is

The voltage V in Fig. is equal to

The voltage V in Fig. is always equal to

The voltage V in Fig. is

In the circuit of Fig. when R = 0 Ω, the current i_R equals 10 A.

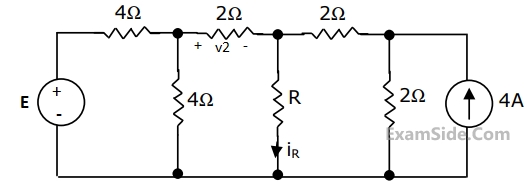
(a) Find the value of R for which it absorbs maximum power.

(b) Find the value of E.

(c) Find v2 when R = $$\infty$$ ( open circuit)

For the circuit shown in Fig. choose state variables $$X_1,\;X_2,\;X_3$$ to be $$i_{L1}\left(t\right),\;v_{C2}\left(t\right),\;i_{L3}\left(t\right)$$

(a) Write the state equations

$$$\begin{bmatrix}{\dot X}_1\\{\dot X}_2\\{\dot X}_3\end{bmatrix}\;=\;A\;\begin{bmatrix}X_1\\X_2\\X_3\end{bmatrix}\;+\;B\left[e\left(t\right)\right]$$$

(b) If e(t) = 0, t $$\geq$$ 0, $$i_{L1}\left(0\right)\;=\;0,\;v_{C2}\left(0\right)\;=\;0,\;i_{L3}\left(0\right)\;=\;1A,$$ then what would the total energy dissipated in the registors in the interval $$\left(0,\infty\right)$$ be

In the circuit of Fig., the current i_D through the ideal diode (zero cut in voltage and zero forward resistance) equals

In the circuit of Fig., energy absorbed by the 4 Ω registor in the time interval (0,$$\infty$$) is

The current "i₄" in the circuit of Fig. is equal to

The function f(t) has the Fourier Transform g($$\omega $$). The Fourier Transform of $$$g(t) = \left( {\int\limits_{ - \infty }^\infty {g(t){e^{ - j\omega t}}} } \right)\,is$$$

The power spectral density of a deterministic signal is given by $${\left[ {\sin (f)/f} \right]^2}$$, where 'f' is frequency. The autocorrelation function of this signal in the time domain is

If the Fourier Transfrom of a deterministic signal g(t) is G (f), then

Item-1
(1) The Fourier transform of g (t - 2) is
(2) The Fourier transform of g (t/2) is

Item - 2
(A) G(f) $$e^{-j\left(4\mathrm{πf}\right)}$$
(B) G(2f)
(C) 2G(2f)
(D) G(f-2)

Match each of the items 1, 2 on the left with the most appropriate item A, B, C or D on the right.

The Laplace Transform of e_at .cos$$\left( {\alpha t} \right).u\left( t \right)$$ is equal to

Match each of the items 1, 2 on the left with the most appropriate item A, B, C or D on the right.

In the case of a linear time invariant system

List - 1
(1) Poles in the right half plane implies.
(2) Impulse response zero for $$t \le 0$$ implies.

List - 2
(A) Exponential decay of output
(B) System is causal
(C) No stored energy in the system
(D) System is unstable

Fig.1, shows the block diagram representation of a control system. The system in block A has an impulse response $${h_A}(t) = {e^{ - t}}\,u(t)$$. The system in block B has an impulse response $${h_B}(t) = {e^{ - 2t}}\,u(t)$$. The block 'k' amplifies its input by a factor k. For the overall system with input x(t) and output y(t)

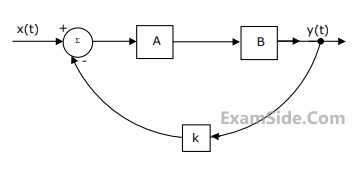
(a) Find the transfer function $${{Y(s)} \over {X(s)}}$$, when k=1

(b) Find the impulse response, when k = 0

(c) Find the value of k for which the system becomes unstable.

$$$\left[ {\matrix{ {Note:u(t)\, \equiv \,0} & {t\, \le \,0} \cr {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \equiv 1} & {t\, > \,0} \cr } } \right]$$$

In Fig. 1, a linear time invariant discrete system is shown. Blocks labeled D represent unit delay elements. For $$n\, < 0,$$ you may assume that $$x\left( n \right),$$ $${y_1}\left( n \right),\,\,{y_2}\left( n \right)$$ are all zero.

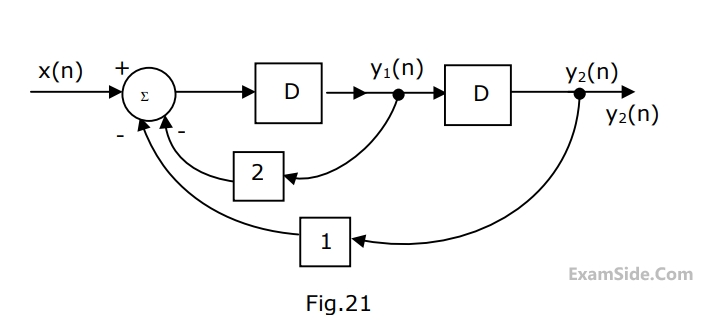
(a) Find the expression for $${y_1}\left( n \right)$$ and $${y_2}\left( n \right)$$ in terms of $$x\left( n \right).$$
(b) Find the transfer function $${y_2}\left( z \right)/X\left( z \right)$$ in the $$z$$-domain.
(c) If $$x\left( n \right) = 1$$ at $$n = 0$$ or $$x\left( n \right) = 0$$ otherwise

Find $${y_2}\left( n \right).$$