Assuming V_Cesat=0.2V and β = 50, the minimum base current (I_B) required to drive the transistor in the figure to saturation is

An ideal Op-Amp is an ideal

In the op-amp circuit given in the figure, the load current i_L is

Voltage series feedback (also called series-shunt feedback) results in

The circuit in the figure is a

The value of 'C' required for a sinusoidal oscillation of frequency 1 KHz in the circuit of the figure is

A bipolar transistor is operating in the active region with a collector current of 1mA. Assuming that the 'β' of the transistor is 100 and the transconductance (g_m) and the input resistance ($${r_\pi }$$) of the transistor in the common emitter configuration, are

In the output of a DM speech encoder, the consecutive pulses are of opposite polarity during time interval t₁ $$ \le $$ t $$ \le $$ t₂. This indicates that during this interval

In a PCM system, if the code word length is increased from 6 to 8 bits, the signal to quantization noise ratio improves by the factor

Consider a binary digital communication system with equally likely $$0’s$$ and $$1’s$$. When binary $$0$$ is transmitted the voltage at the detector input can lie between the levels $$-0.25V$$ and $$+0.25V$$ with equal probability when binary $$1$$ is transmitted, the voltage at the detector can have any value between $$0$$and $$1 V$$ with equal probability. If the detector has a threshold of $$2.0V$$ (i.e., if the received signal is greater than $$0.2 V$$, the bit is taken as $$1$$), the average bit error probability is

Choose the correct one from among the alternatives A, B, C, D after matching an item from Group 1 with the most appropriate item in Group 2.

Group
1. FM
2. DM
3. PSK
4. PCM

Group 2
P: Slope overload
Q: $${\mu - law}$$
R: Envelope detector
S: Capture effect
T: Hilbert transform
U: Matched filter

A source produces binary data at the rate of 10 kbps. The binary symbols are represented as shown in fig. The source output is transmitted using two modulation schemes, namely Binary PSK (BPSK) and Quadrature PSK (QPSK). Let $${B_1}$$ and $${B_2}$$ be the bandwidth requirements of BPSK and QPSK respectively. Assuming that the bandwidth of the above rectangular pulses is 10 kHz, $${B_1}$$ and $${B_2}$$ are

Three analog signals, having bandwidths 1200 Hz, 600 Hz and 600 Hz are sampled at their respective Nyquist rates, enocodes with 12 bit words, and time division multiplexed. The bit rate for the multiplexed signal is

A 1 mW video signal having a bandwidth of 100 MHz is transmitted to a receiver through a cable that has 40 dB loss. If the effective one-sided noise spectral density at the receiver is 10^-20 Watt/Hz, then the signal-to-noise ratio at the receiver is

Two sinusoidal signals of same amplitude and frequencies 10 kHz and 10.1 kHz are added together. The combined signal is given to an ideal frequency detector. The output of the detector is

An AM signal and a narrow-band FM signal with identical carriers, modulating signals and modulation indices of 0.1 are added together. The resultant signal can be closely approximated by

An AM signal is detected using an envelope detector. The carrier frequency and modulating signal frequency are 1 MHz and 2 KHz respectively. An appropriate value for the time constant of the envelope detector is

A system described by the following differential equation $$$\frac{d^2y}{dt^2}+3\frac{dy}{dt}+2y=x\left(t\right)$$$ is initially at rest. For input x(t) = 2u(t), the output y(t) is

Consider the signal flow graph shown in Figure. The gain $$\frac{x_5}{x_1}$$ is

Consider the Bode magnitude plot shown in figure. The transfer function H(s) is

For the polynomial
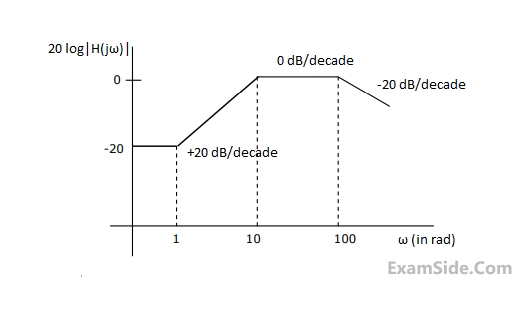
P(s) = s⁵ + s⁴ + 2s³ + 2s² + 3s + 15 ,
the number of roots which lie in the right half of the s-plane is

A causal system having the transfer function $$G\left(s\right)\;=\;\frac1{s\;+\;2}$$ is excited with 10u(t). The time at which the output reaches 99% of its steady state value is

Given A $$ = \left[ {\matrix{ 1 & 0 \cr 0 & 1 \cr } } \right],$$ the state transition matrix e^At is given by

If A = $$\left[ {\matrix{ { - 2} & 2 \cr 1 & { - 3} \cr } } \right],$$ then sin At is

The state variable equations of a system are: $$${\mathop {{x_1} = - 3{x_1} - x}\limits^ \bullet _2} + u$$$ $$${\mathop x\limits^ \bullet _2} = 2{x_1}$$$ $$$y = {x_1} + u.$$$
The system is

A system has poles at 0.01 Hz, 1Hz and 80 Hz; zeroes at 5hz, 100 Hz and 200 Hz. The approximate phase of the system response at 20 Hz is

Figure shows the internal schematic of a TTL AND-OR-Invert (AOI) gate. For the inputs shown in Figure, the output Y is

11001, 1001 and 111001 correspond to the 2’s complement representation of which one of the following sets of number?

The range of signed decimal numbers that can be represented by 6-bite 1’s complement number is

In the modulo-6 ripple counter shown in the figure, the output of the 2-input gate is used to clear the J-K flip-flops. The 2-input gate is

Choose the correct one from among the alternatives A, B, C, D after matching an item from Group 1 with the most appropriate item in Group 2.

Group1
P. shift register
Q. Counter
R. Decoder

Group2
1. Frequency division
2. Addressing in memory chips
3. Serial to parallel data conversion

A master slave flip-flop has the characteristic that

The minimum number of 2 to 1 multiplexers required to realize a 4 to 1 mutliplexer is

A Boolean function 'f' of two variables x and y is defined as follows: f(0,0)=f(0,1)=f(1,1)=1;f(1,0)=0 Assuming complements of x and y are not available, a minimum cost solution for realizing F using only 2-input NOR gates and 2-input OR gates (each having unit cost) would have a total cost

The Boolean expression AC + B$$\overline C $$ is equivalent to

Consider an impedance Z = R + jX marked with point P in an impedance Smith chart as shown in Fig. The movement from point P along a constant resistance circle in the clockwise direction by an angle $${45^ \circ }$$ is equivalent to

Consider a lossless antenna with a directive gain of + 6 dB. If 1 m W of power is fed to it the total power radiated by the antenna will be

The phase velocity of an electromagnetic wave propagating in a hollow metallic rectangular waveguide in the $$T{E_{10}}$$ mode is

A plane electromagnetic wave propagating in free space in incident normally on a large slab of loss-less, non-magnetic, dielectric material with $$\varepsilon > {\varepsilon _0}$$. Maxima and minima are observed when the electric field is measured in front of the slab. The maximum electric field is found to be $$5$$ times the minimum field. The intrinsic impedance of the medium should be

Consider a 300$$\Omega $$, quarter-wave long (at 1 GHz) transmission line as shown in Fig. It is connected to a 10V, 50$$\Omega $$ sources at one end and is left open circuited at the other end. The magnitude of the voltage at the open circuit end of the line is

A lossless transmission line is terminated in a load which reflects a part of the incident power. The measured VSWR is 2. The percentage of the power that is reflected back is

The drain of an n-channel MOSFET is shorted to the gate so that V_GS = V_DS. The threshold voltage (V_T) of MOSFET is 1 V. If the drain current (I_D) is 1 mA for V_GS = 2 V, then for V_GS = 3 V, I_D is

Consider the following statements S1 and S2.

S1: The threshold voltage (V_T) of a MOS capacitor decreases with increase in gate oxide thickness

S2: The threshold voltage (V_T) of a MOS capacitor decreases with increase in substrate doping concentration.

Which one of the following is correct?

The impurity commonly used for realizing the base region of a silicon n-p-n transistor is

Consider the sequence of 8085 instructions given below.
LXI H, 9258
MOV A, M
CMA
MOV M, A
Which one of the following is performed by this sequence?

It is desired to multiply the numbers 0AH by 0BH and store the result in the accumulator. The numbers are available in registers B and C respectively. A part of the 8085 program for this purpose is given below:
MVI A, 00H
LOOP:.........
...............
HLT END

The sequence of instruction to be complete the program would be

The number of memory cycles required to execute the following 8085 instructions
(I.) LDA 3000H
(II.) LXI D, FOF 1H
Would be

The 8255 Programmable Peripheral Interface is used as described below.

I. An A/D converter is interfaced to a microprocessor through an 8255. the conversion is initiated by a signal from the 8255 on Port C. A signal on Port C causes data to be strobed into Port A.

II. Two computers exchange data using a pair of 8255s. Port A works as a bidirectional data port supported by appropriate handshaking signals.

The appropriate modes of operation of the 8255 for I and II would be

For the circuit shown in Figure, the initial conditions are zeros. Its transfer function $$H(s) = {{{V_c}\,(s)} \over {{V_i}\,(s)}}$$ is

For the lattice circuit shown in Fig., $${Z_a} = j\,2\,\Omega \,\,and\,\,{Z_b} = \,\,2\Omega $$. The values of the open circuit impedance parameters
$$Z\,\left[ {\matrix{ {{Z_{11}}} & {{Z_{12}}} \cr {{Z_{21}}} & {{Z_{22}}} \cr } } \right]\,$$ are

The transfer function $$H\left( s \right) = {{{V_0}\left( s \right)} \over {{V_i}\left( s \right)}}$$ of an R-L-C circuit is given by
$$H\left( s \right) = {{{{10}^6}} \over {{s^2} + 20s + {{10}^6}}}$$

The Quality factor (Q-factore) of this circuit is

The circuit shown in figure, with $$R = 1/3\Omega $$, $$L = 1/4H$$, $$C = 3F$$ has input voltage $$v\left( t \right) = \sin \,2t$$. The resulting current $$i(t)$$ is

For the circuit shown in figure, the time constant $$RC = 1$$ $$ms$$. The input voltage is $${v_i}\left( t \right) = \sqrt 2 \,\sin \,{10^3}t$$. The output voltage $${v_0}\left( t \right)$$ is equal to

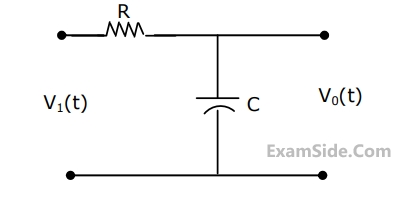
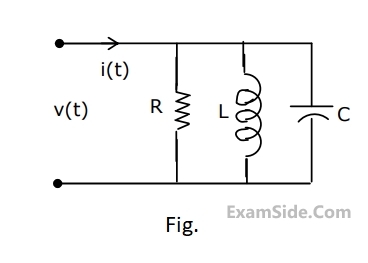
Consider the following statements S1 and S2.

S₁: The $$\beta$$ of a bipolar transistor reduces if the base width is increased.

S₂: The $$\beta$$ of a bipolar transistor increases if the doping concentration in the base in increased

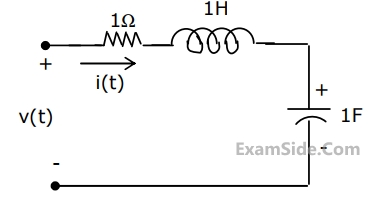
Which one of the following is correct?

The circuit shown in Fig, has initial current $${\mathrm i}_\mathrm L\left(0^-\right)\;=\;1\;\mathrm A$$ through the inductor and an initial voltage $${\mathrm v}_\mathrm C\left(0^-\right)\;=\;-1\;\mathrm V$$ across the capacitor. For input v(t) = u(t), the Laplace transform of the current i(t) for t ≥ 0 is

For the R-L circuit shown in Fig, the input voltage. v_i(t) = u (t) The current i(t) is

The equivalent inductance measured between the terminals 1 and 2 for the circuit shown in figure, is

Let x(t) and y(t) (with Fourier transforms X(f) and Y(f) respectively) be related as shown in Fig.(1) & (2).

Then Y(f) is

A 1 kHz sinusoidal signal is ideally sampled at 1500 samples /sec and the sampled signal is passed through an ideal low-pass filter with cut-off frequency 800 Hz. The output signal has the frequency

Consider the signal x(t) shown in Fig. Let h(t) denote the impulse response of the filter matched to x(t), with h(t) being non-zero only in the interval 0 to 4 sec. The slope of h(t) in the interval 3 < t < 4 sec is

A system has poles at 0.01 Hz, 1 Hz and 80 Hz; zeros at 5 Hz, 100 Hz and 200 Hz. The approximate phase of the system response at 20 Hz is

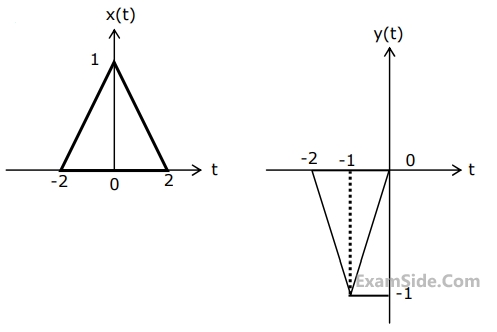
The impulse response $$h\left[ n \right]$$ of a linear time invariant system is given as
$$h\left[ n \right] = \left\{ {\matrix{ { - 2\sqrt 2 ,} & {n = 1, - 1} \cr {4\sqrt 2 ,} & {n = 2, - 2} \cr {0,} & {otherwise} \cr } } \right.$$

If the input to the above system is the sequence $${e^{j\pi n/4}},$$ then the output is

A causal LTI system is described by the difference equation $$2y\left[ n \right] = ay\left[ {n - 2} \right] - 2x\left[ n \right] + \beta x\left[ {n - 1} \right].$$ The system is stable only if

The impulse response $$h\left[ n \right]$$ of a linear time-invariant system is given by $$h\left[ n \right]$$ $$ = u\left[ {n + 3} \right] + u\left[ {n - 2} \right] - 2\,u\left[ {n - 7} \right],$$ where $$u\left[ n \right]$$ is the unit step sequence. The above system is

Consider the sequence

$$x[n] = [ - \,4 - \,j5,\,\mathop {1 + j2}\limits_ \uparrow ,\,\,4]$$

The conjugate anti-symmetric part of the sequence is

A causal system having the transfer function H(s) = $${1 \over {s + 2}}$$, is excited with 10 u(t). The time at which the output reaches 99% of its steady state value is

A rectangular pulse train s(t) as shown in Fig.1 is convolved with the signal $${\cos ^2}$$ ($$4\pi \,{10^{3\,}}$$t). The convolved signal will be a

A system described by the differential equation: $${{{d^2}y} \over {d{t^2}}} + 3{{dy} \over {dt}} + 2y = x(t)$$ is initially at rest. For input x(t) = 2u(t), the output y(t) is

The z transform of a system is
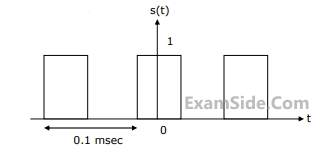
H(z) = $${z \over {z - 0.2}}$$ .
If the ROC is $$\left| {z\,} \right|$$ < 0.2, then the impulse response of the system is

The Fourier transform of a conjugate symmetric function is always