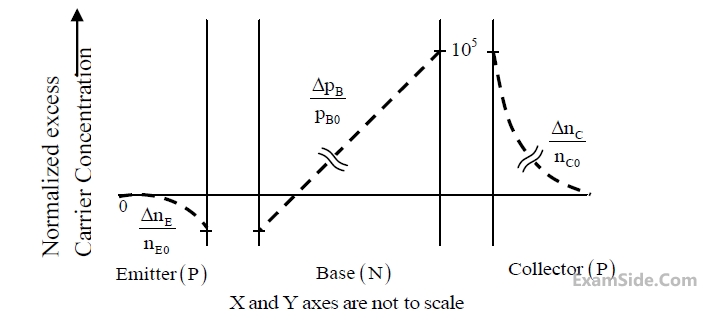
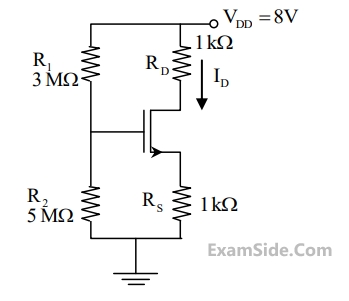
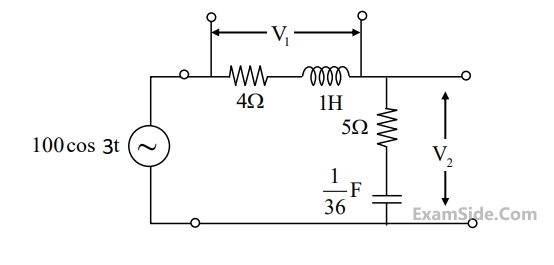
GATE ECE
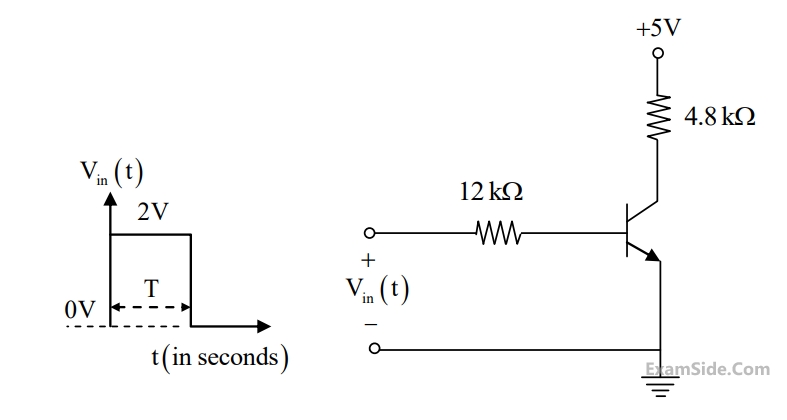
For the input vin(t)as shown in the figure, the transistor switches between the cut-off and saturation regions of operation, when T is large. Assume collector-to-emitter voltage saturation VCE(sat) = 0.2V and base-to-emitter voltage VBE = 0.7V. The minimum value of the common-base current gain$$\left( \alpha \right)$$ of the transistor for the switching should be _________.
As shown in Figure (b). The output of the low pass filter is $$y(t)$$.
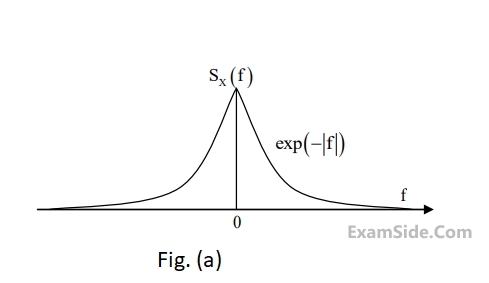
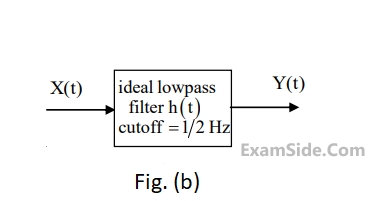
Let $$E$$ be the expectation operator and consider the following statements :
$$\left( {\rm I} \right)$$ $$E\left( {X\left( t \right)} \right) = E\left( {Y\left( t \right)} \right)$$
$$\left( {{\rm I}{\rm I}} \right)$$ $$\,\,\,\,\,\,\,\,E\left( {{X^2}\left( t \right)} \right) = E\left( {{Y^2}\left( t \right)} \right)$$
$$\left( {{\rm I}{\rm I}{\rm I}} \right)\,$$ $$\,\,\,\,\,\,E\left( {{Y^2}\left( t \right)} \right) = 2$$
Select the correct option:
$$\,{u_o}(t) = 5\,\cos \,(20000\,\pi \,t);\,0 \le \,\,t\, \le \,T,$$ and
$${u_o}(t) = 5\,\cos \,(22000\,\pi \,t);\,0 \le \,\,t\, \le \,T,$$
where T is the bit-duration interval and t is in seconds. Both $${u_o}(t)$$ and $${u_1}(t)$$ are zero output the interval $$0 \le \,\,t\, \le \,T$$. With a matched filter (correlator ) based receiver, the smallest positive value of T (in milliseconds) required to have $${u_o}(t)$$ and $${u_1}(t)$$ uncorrelated is
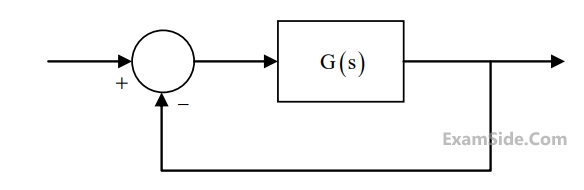 Given that the steady state error is zero for unit step input and is 6 for unit ramp input, the
value of the parameter p is _________.
Given that the steady state error is zero for unit step input and is 6 for unit ramp input, the
value of the parameter p is _________.

For the closed loop system shown, the root locus for 0 < K < $$\infty$$ intersects the imaginary axis for K = 1.5. The closed loop system is stable for
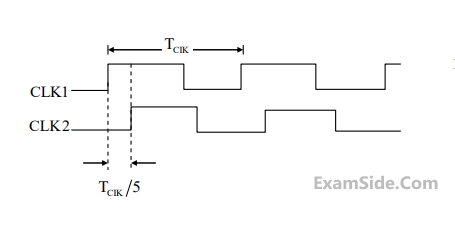
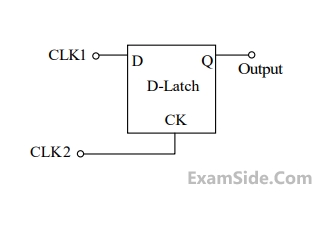
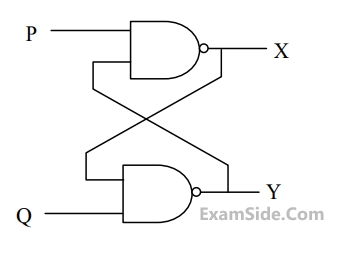

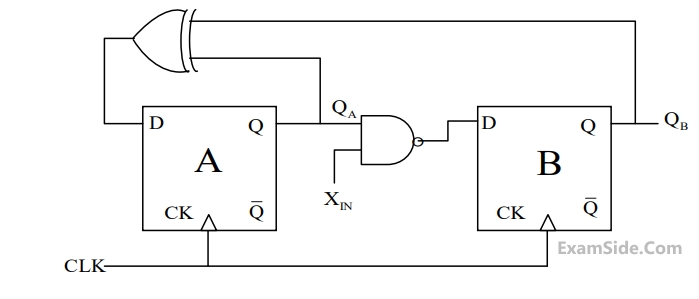
Assume that XIN is held at a logic level throughout the operation of the FSM. When the FSM is initialized to the state QA QB = 100 and clocked, after a few clock cycles, it starts cycling through
It is given that $$A$$ has only one real eigen value. Then the real eigen value of $$A$$ is
Where $$x, y, z$$ are real. The volume of $$R$$ correct to two decimal places is __________.
$$\,\,\overrightarrow F = \widehat a{}_x\left( {3y - k{}_1z} \right) + \widehat a{}_y\left( {k{}_2x - 2z} \right) - \widehat a{}_z\left( {k{}_3y + z} \right)\,\,\,$$
is irrotational, then the values of the constants $$\,{k_1},\,{k_2}\,\,$$ and $$\,{k_3}$$ respectively, are
$${\rm I}.\,\,\,\,\,$$ $${y_1},{y_2}$$ and $${y_3}$$ are linearly independent on $$ - 1 \le x \le 0$$
$${\rm II}.\,\,\,\,\,$$ $${y_1},{y_2}$$ and $${y_3}$$ are linearly dependent on $$0 \le x \le 1$$
$${\rm III}.\,\,\,\,\,$$ $${y_1},{y_2}$$ and $${y_3}$$ are linearly independent on $$0 \le x \le 1$$
$${\rm IV}.\,\,\,\,\,$$ $${y_1},{y_2}$$ and $${y_3}$$ are linearly dependent on $$ - 1 \le x \le 0$$
Which one among the following is correct?
MVI A, 33H
MVI B, 78H
ADD B
CMA
ANI 32H
The Accumulator value immediately after the execution of the fifth instruction is
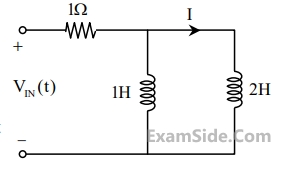
where $$'t'$$ is in seconds. The time (in seconds) at which the current $${\rm I}$$ in the circuit will reach the value $$2$$ Ampere is ______ .
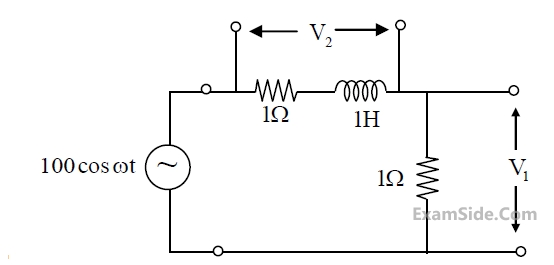
$$y\left[ n \right]\, = \left\{ {\matrix{ {n\left| {x\left[ n \right]} \right|,} & {for\,\,0 \le n \le 10} \cr {x\left[ n \right] - x\left[ {n - 1} \right],} & {otherwise,} \cr } } \right.$$
Which one of the following statements is true about the system?
Let y(t) be the output of this filter. The maximum value of $$\left| {y(t)} \right|$$ is ________________________.
I. The complex Fourier series coefficients of x(3t) are {ak} where k is integer valued
II. The complex Fourier series coefficients of x(3t) are {3ak} where k is integer valued
III. The fundamental angular frequency of x(3t) is 6$$\mathrm\pi$$ rad/s
For the three statements above, which one of the following is correct?I. There is no bounded input bounded output (BIBO) stable system with a pole in the right half of the complex plane.
II. There is no causal and BIBO stable system with a pole in the right half of the complex plane.
Which one among the following is correct?
General Aptitude
Here, the word ‘antagonistic’ is closest in meaning to

The path from P to Q is best described by
Which of the following statement is correct?
(i) At least one bench is a table
(ii) At least one shelf is a bench
(iii) At least one chair is a table
(iv) All benches are chairs