Let g(t) = $${e^{ - \pi {t^2}}}$$, and h(t) is a filter matched to g(t). If g(t) is applied as input to h(t), then the Fourier transform of the output is

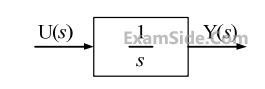
Assuming zero initial condition, the response y (t) of the system given below to a unit step input u(t) is

A system with the transfer function $${{Y(s)} \over {X(s)}} = {s \over {s + p}}\,\,$$ has an output
$$y(t) = \cos \left( {2t - {\pi \over 3}} \right)\,$$ for the input signal
$$x(t) = p\cos \left( {2t - {\pi \over 2}} \right)$$. Then, the system parameter 'p' is

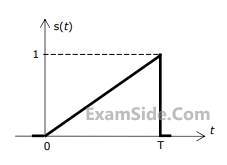
Consider the pulse shape s(t) as shown. The impulse response h(t) of the filter matched to this pulse is