1
GATE ECE 2005
MCQ (Single Correct Answer)
+2
-0.6
In what range should Re(s) remain so that the Laplace transform of the function e(a+2)t+5 exists?
2
GATE ECE 2002
MCQ (Single Correct Answer)
+2
-0.6
The Laplace transform of a continuous - time signal x(t) is $$X\left( s \right) = {{5 - s} \over {{s^2} - s - 2}}$$. If the Fourier transform of tyhis signal exists, then x(t) is
3
GATE ECE 1996
MCQ (Single Correct Answer)
+2
-0.6
The inverse Laplace transform of the function $${{s + 5} \over {\left( {s + 1} \right)\left( {s + 3} \right)}}$$ is
4
GATE ECE 1993
Fill in the Blanks
+2
-0
The Laplace transform of the periodioc function f(t) describe4d by the curve below, i.e.,
$$f\left( t \right) = \left\{ {\matrix{
{\sin \,t\,\,\,if\,\left( {2n - 1} \right)\pi \le t \le 2n\pi } \cr
{0\,\,\,\,\,\,\,\,otherwise} \cr
} } \right.$$
is _________. (fill in the blank), n is an integer.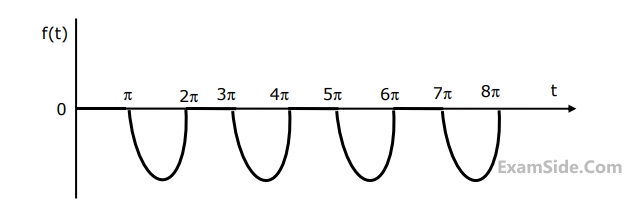
is _________. (fill in the blank), n is an integer.

Questions Asked from Continuous Time Signal Laplace Transform (Marks 2)
Number in Brackets after Paper Indicates No. of Questions
GATE ECE 2016 Set 1 (1)
GATE ECE 2015 Set 2 (1)
GATE ECE 2015 Set 1 (1)
GATE ECE 2014 Set 1 (1)
GATE ECE 2014 Set 4 (3)
GATE ECE 2014 Set 3 (1)
GATE ECE 2013 (1)
GATE ECE 2011 (1)
GATE ECE 2010 (1)
GATE ECE 2009 (1)
GATE ECE 2006 (1)
GATE ECE 2005 (1)
GATE ECE 2002 (1)
GATE ECE 1996 (1)
GATE ECE 1993 (2)
GATE ECE 1988 (1)
GATE ECE 1987 (1)
GATE ECE Subjects
Signals and Systems
Representation of Continuous Time Signal Fourier Series Fourier Transform Continuous Time Signal Laplace Transform Discrete Time Signal Fourier Series Fourier Transform Discrete Fourier Transform and Fast Fourier Transform Discrete Time Signal Z Transform Continuous Time Linear Invariant System Discrete Time Linear Time Invariant Systems Transmission of Signal Through Continuous Time LTI Systems Sampling Transmission of Signal Through Discrete Time Lti Systems Miscellaneous
Network Theory
Control Systems
Digital Circuits
General Aptitude
Electronic Devices and VLSI
Analog Circuits
Engineering Mathematics
Microprocessors
Communications
Electromagnetics