1
GATE ECE 2010
MCQ (Single Correct Answer)
+1
-0.3
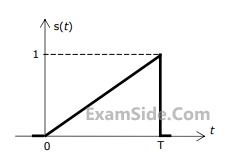
Consider the pulse shape s(t) as shown. The impulse response h(t) of the filter matched to this pulse is

2
GATE ECE 2006
MCQ (Single Correct Answer)
+1
-0.3
A low-pass filter having a frequency response $$H(j\omega )$$ = $$A(\omega ){e^{j\Phi (\omega )}}$$, does not product any phase distortion if
3
GATE ECE 2006
MCQ (Single Correct Answer)
+1
-0.3
In the system shown below,
x(t) = (sint)u(t). In steady-state, the response y(t) will be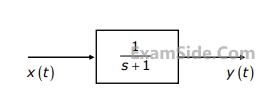
x(t) = (sint)u(t). In steady-state, the response y(t) will be

4
GATE ECE 2002
MCQ (Single Correct Answer)
+1
-0.3
A linear phase channel with phase delay $${\tau _p}$$ and group delay $${\tau _g}$$ must have
Questions Asked from Transmission of Signal Through Continuous Time LTI Systems (Marks 1)
Number in Brackets after Paper Indicates No. of Questions
GATE ECE Subjects
Signals and Systems
Representation of Continuous Time Signal Fourier Series Discrete Time Signal Fourier Series Fourier Transform Discrete Time Signal Z Transform Continuous Time Linear Invariant System Transmission of Signal Through Continuous Time LTI Systems Discrete Time Linear Time Invariant Systems Sampling Continuous Time Signal Laplace Transform Discrete Fourier Transform and Fast Fourier Transform Transmission of Signal Through Discrete Time Lti Systems Miscellaneous Fourier Transform
Network Theory
Control Systems
Digital Circuits
General Aptitude
Electronic Devices and VLSI
Analog Circuits
Engineering Mathematics
Microprocessors
Communications
Electromagnetics



