Consider a base band binary PAM receiver shown below. The additive channel noise $$n(t)$$ is white with power spectral density $${S_N}\left( f \right) = {N_0}/2 = {10^{ - 20}}$$ $$W/Hz$$. The low-pass filter is ideal with unity gain and cut -off frequency $$1MHz$$. Let $${Y_k}$$ represent the random variable $$y\left( {{t_k}} \right)$$.
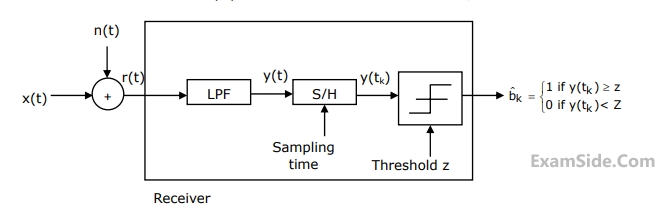
$${Y_k} = {N_k}$$ if transmitted bit $${b_k} = 0$$
$${Y_k} = a + {N_k}$$ if transmitted bit $${b_k} = 1$$
Where $${b_k} = 0$$ represents the noise sample value. The noise sample has a probability density function, $${P_{{N_k}}}\left( n \right)\,\,\,\,\,\,\, = 0.5\alpha {e^{ - \alpha \left| n \right|}}$$ (This has mean zero and variance $$2/{\alpha ^2}$$). Assume transmitted bits to be equiprobable and threshold $$z$$ is set to $$a/2 = {10^{ - 6}}V$$.

The probability of bit error is

The amplitude of random signal is uniformly distributed between $$-$$5V and 5V

If the signal to quantization noise ratio required in uniformly quantizing the signals is 43.5 dB, the step size of the quantization is approximately

The amplitude of random signal is uniformly distributed between $$-$$5V and 5V

If the positive values of the signal are uniformly quantized with a step size of 0.05 V, and the negative values are uniformly quantized with a step size of 0.1V, the resulting signal to quantization noise ratio is approximately

Consider a Binary Symmetric Channel (BSC) with probability of error being 'p'. To transit a bit, say 1, we transmit a sequence of three 1s. The receiver will interpret the received sequence to represent 1 if at least two bits are 1. The probability that the transmitted bit will be received in error is