JEE Advanced 2017 Paper 2 Offline
Paper was held on
Sun, May 21, 2017 2:00 AM
Chemistry
1
Pure water freezes at $$273$$ $$K$$ and $$1$$ bar. The addition of $$34.5$$ $$g$$ of ethanol to $$500$$ $$g$$ of water changes the freezing point of the solution. Use the freezing point depression constant of water as $$2$$ kg $$mo{l^{ - 1}}.$$ The figures shown below represent plots of vapor pressure $$(V.P.)$$ versus temperature $$(T).$$ [molecular weight of ethanol is $$46$$ $$g$$ $$mo{l^{ - 1}}.$$ ] Among the following, the option representing change in the freezing point is
2
The product $$S$$ is
3
The order of basicity among the following compounds is


4
$$Y$$ and $$Z$$ are, respectively
5
Which of the following combination will produce $${H_2}$$ gas ?
6
For the following compounds, the correct statement(s) with respect to nucleophilic substitution reaction is (are)


7
For the following cell,
$$Zn\left( s \right)\left| {ZnS{O_4}\left( {aq} \right)} \right|\left| {CuS{O_4}\left( {aq} \right)} \right|Cu\left( s \right)$$
when the concentration of $$Z{n^{2 + }}$$ is $$10$$ times the concentration of $$C{u^{2 + }},$$ the expression for $$\Delta G$$ (in $$J\,mo{l^{ - 1}}$$) is [$$F$$ is Faraday constant; $$R$$ is gas constant; $$T$$ is temperature; $${E^0}$$ (cell)$$=1.1$$ $$V$$]
$$Zn\left( s \right)\left| {ZnS{O_4}\left( {aq} \right)} \right|\left| {CuS{O_4}\left( {aq} \right)} \right|Cu\left( s \right)$$
when the concentration of $$Z{n^{2 + }}$$ is $$10$$ times the concentration of $$C{u^{2 + }},$$ the expression for $$\Delta G$$ (in $$J\,mo{l^{ - 1}}$$) is [$$F$$ is Faraday constant; $$R$$ is gas constant; $$T$$ is temperature; $${E^0}$$ (cell)$$=1.1$$ $$V$$]
8
The standard state Gibbs free energies of formation of $$C$$(graphite) and $$C$$(diamond) at $$T=298$$ $$K$$ are
$${\Delta _f}{G^0}$$ [$$C$$(graphite)] $$ = 0kJmo{l^{ - 1}}$$
$${\Delta _f}{G^0}$$ [$$C$$(diamond)] $$ = 2.9kJmo{l^{ - 1}}$$
The standard state means that the pressure should be $$1$$ bar, and substance should be pure at a given temperature. The conversion of graphite [$$C$$(graphite)] to diamond [$$C$$(diamond)] reduces its volume by $$2 \times {10^{ - 6}}\,{m^3}\,mo{l^{ - 1}}$$ If $$C$$(graphite) is converted to $$C$$(diamond) isothermally at $$T=298$$ $$K,$$ the pressure at which $$C$$(graphite) is in equilibrium with $$C$$(diamond), is
[Useful information : $$1$$ $$J=1$$ $$kg\,{m^2}{s^{ - 2}};1\,Pa = 1\,kg\,{m^{ - 1}}{s^{ - 2}};$$ $$1$$ bar $$ = {10^5}$$ $$Pa$$]
$${\Delta _f}{G^0}$$ [$$C$$(graphite)] $$ = 0kJmo{l^{ - 1}}$$
$${\Delta _f}{G^0}$$ [$$C$$(diamond)] $$ = 2.9kJmo{l^{ - 1}}$$
The standard state means that the pressure should be $$1$$ bar, and substance should be pure at a given temperature. The conversion of graphite [$$C$$(graphite)] to diamond [$$C$$(diamond)] reduces its volume by $$2 \times {10^{ - 6}}\,{m^3}\,mo{l^{ - 1}}$$ If $$C$$(graphite) is converted to $$C$$(diamond) isothermally at $$T=298$$ $$K,$$ the pressure at which $$C$$(graphite) is in equilibrium with $$C$$(diamond), is
[Useful information : $$1$$ $$J=1$$ $$kg\,{m^2}{s^{ - 2}};1\,Pa = 1\,kg\,{m^{ - 1}}{s^{ - 2}};$$ $$1$$ bar $$ = {10^5}$$ $$Pa$$]
9
The order of the oxidation state of the phosphorous atom in
$${H_3}P{O_2},{H_3}P{O_4},{H_3}P{O_3}$$ and $${H_4}{P_2}{O_6}$$ is
$${H_3}P{O_2},{H_3}P{O_4},{H_3}P{O_3}$$ and $${H_4}{P_2}{O_6}$$ is
10
For a reaction taking place in a container in equilibrium with its surroundings, the effect of temperature on its equilibrium constant $$K$$ in terms of change in entropy is described by
11
The correct statement(s) about surface properties is (are)
12
In a bimolecular reaction, the steric factor $$P$$ was experimentally determined to be $$4.5.$$ The correct option(s) among the following is (are)
13
Among the following, the correct statement(s) is (are)
14
The options(s) with only amphoteric oxides is (are)
15
Compounds $$P$$ and $$R$$ upon ozonolysis produce $$Q$$ and $$S,$$ respectively. The molecular formula of $$Q$$ and $$S$$ is $${C_8}{H_8}O.Q$$ undergoes Canninzzaro reaction but not haloform reaction, whereas $$S$$ undergoes haloform reaction but not Cannizzaro reaction

The option(s) with suitable combination of $$P$$ and $$R,$$ respectively, is (are)

The option(s) with suitable combination of $$P$$ and $$R,$$ respectively, is (are)
16
$$W$$ and $$X$$ are, respectively
17
The reactions, $$Q$$ to $$R$$ and $$R$$ to $$S,$$ are
18
The major product of the following reaction is


Mathematics
1
If f : R $$ \to $$ R is a twice differentiable function such that f"(x) > 0 for all x$$ \in $$R, and $$f\left( {{1 \over 2}} \right) = {1 \over 2}$$, f(1) = 1, then
2
If y = y(x) satisfies the differential equation
$${8\sqrt x \left( {\sqrt {9 + \sqrt x } } \right)dy = {{\left( {\sqrt {4 + \sqrt {9 + \sqrt x } } } \right)}^{ - 1}}}$$
dx, x > 0 and y(0) = $$\sqrt 7 $$, then y(256) =
$${8\sqrt x \left( {\sqrt {9 + \sqrt x } } \right)dy = {{\left( {\sqrt {4 + \sqrt {9 + \sqrt x } } } \right)}^{ - 1}}}$$
dx, x > 0 and y(0) = $$\sqrt 7 $$, then y(256) =
3
How many 3 $$ \times $$ 3 matrices M with entries from {0, 1, 2} are there, for which the sum of the diagonal entries of MTM is 5?
4
Three randomly chosen nonnegative integers x, y and z are found to satisfy the equation x + y + z = 10. Then the probability that z is even, is
5
Let S = {1, 2, 3, .........., 9}. For k = 1, 2, .........., 5, let Nk be the number of subsets of S, each containing five elements out of which exactly k are odd. Then N1 + N2 + N3 + N4 + N5 =
6
Let O be the origin and let PQR be an arbitrary triangle. The point S is such that
$$\overrightarrow{OP}$$ . $$\overrightarrow{OQ}$$ + $$\overrightarrow{OR}$$ . $$\overrightarrow{OS}$$ = $$\overrightarrow{OR}$$ . $$\overrightarrow{OP}$$ + $$\overrightarrow{OQ}$$ . $$\overrightarrow{OS}$$ = $$\overrightarrow{OQ}$$ . $$\overrightarrow{OR}$$ + $$\overrightarrow{OP}$$ . $$\overrightarrow{OS}$$
Then the triangle PQR has S as its
$$\overrightarrow{OP}$$ . $$\overrightarrow{OQ}$$ + $$\overrightarrow{OR}$$ . $$\overrightarrow{OS}$$ = $$\overrightarrow{OR}$$ . $$\overrightarrow{OP}$$ + $$\overrightarrow{OQ}$$ . $$\overrightarrow{OS}$$ = $$\overrightarrow{OQ}$$ . $$\overrightarrow{OR}$$ + $$\overrightarrow{OP}$$ . $$\overrightarrow{OS}$$
Then the triangle PQR has S as its
7
The equation of the plane passing through the point (1, 1, 1) and perpendicular to the planes 2x + y $$-$$ 2z = 5 and 3x $$-$$ 6y $$-$$ 2z = 7 is
8
f : R $$ \to $$ R is a differentiable function such that f'(x) > 2f(x) for all x$$ \in $$R, and f(0) = 1 then
9
If $$I = \sum\nolimits_{k = 1}^{98} {\int_k^{k + 1} {{{k + 1} \over {x(x + 1)}}} dx} $$, then
10
If the line x = $$\alpha $$ divides the area of region R = {(x, y) $$ \in $$R2 : x3 $$ \le $$ y $$ \le $$ x, 0 $$ \le $$ x $$ \le $$ 1} into two equal parts, then
11
Let $$\alpha $$ and $$\beta $$ be non zero real numbers such that $$2(\cos \beta - \cos \alpha ) + \cos \alpha \cos \beta = 1$$. Then which of the following is/are true?
12
Let $$f(x) = {{1 - x(1 + |1 - x|)} \over {|1 - x|}}\cos \left( {{1 \over {1 - x}}} \right)$$
for x $$ \ne $$ 1. Then
for x $$ \ne $$ 1. Then
13
If $$g(x) = \int_{\sin x}^{\sin (2x)} {{{\sin }^{ - 1}}} (t)\,dt$$, then
14
If $$f(x) = \left| {\matrix{
{\cos 2x} & {\cos 2x} & {\sin 2x} \cr
{ - \cos x} & {\cos x} & { - \sin x} \cr
{\sin x} & {\sin x} & {\cos x} \cr
} } \right|$$,
then
then
15
If the triangle PQR varies, then the minimum value of cos(P + Q) + cos(Q + R) + cos(R + P) is
16
|$$\overrightarrow{OX}$$ $$ \times $$ $$\overrightarrow{OY}$$| = ?
17
a12 = ?
18
If a4 = 28, then p + 2q =
Physics
1
A point charge $$+Q$$ is placed just outside an imaginary hemispherical surface of radius $$R$$ as shown in the figure. Which of the following statements is/are correct?


2
Two coherent monochromatic point sources $${S_1}$$ and $${S_2}$$ of wavelength $$\lambda = 600\,nm$$ are placed symmetrically on either side of the center of the circle as shown. The sources are separated by a distance $$d=1.8$$ $$mm.$$ This arrangement produces interference fringes visible as alternate bright and dark spots on the circumference of the circle. The angular separation between two consecutive bright spots is $$\Delta \theta .$$ Which of the following options is/are correct?


3
The instantaneous voltages at three terminals marked $$X,Y$$ and $$Z$$ are given by
$${V_x} = {V_0}\,\sin \,\omega t,$$
$${V_Y} = {V_0}\,\sin $$ $$\left( {\omega t + {{2\pi } \over 3}} \right)$$
and $$Vz = {V_0}\sin \left( {\omega t + {{4\pi } \over 3}} \right)$$
An ideal voltmeter is configured to read $$rms$$ value of the potential difference between its terminals. It is connected between points $$X$$ and $$Y$$ and then between $$Y$$ and $$Z.$$ The reading(s) of the voltmeter will be
$${V_x} = {V_0}\,\sin \,\omega t,$$
$${V_Y} = {V_0}\,\sin $$ $$\left( {\omega t + {{2\pi } \over 3}} \right)$$
and $$Vz = {V_0}\sin \left( {\omega t + {{4\pi } \over 3}} \right)$$
An ideal voltmeter is configured to read $$rms$$ value of the potential difference between its terminals. It is connected between points $$X$$ and $$Y$$ and then between $$Y$$ and $$Z.$$ The reading(s) of the voltmeter will be
4
A uniform magnetic field $$B$$ exist in the region between $$x=0$$ and $$x = {{3R} \over 2}$$ (region $$2$$ in the figure) pointing normally into the plane of the paper. A particle with charge $$+Q$$ and momentum $$p$$ directed along $$x$$-axis enters region $$2$$ from region $$1$$$ at point $${P_1}\left( y \right) = - R).$$ Which of the following option(s) is/are correct?


5
A person measures the depth of a well by measuring the time interval between dropping a stone and receiving the sound of impact with the bottom of the well. The error in his measurement of time is $$\delta T = 0.01$$ seconds and he measures the depth of the well to be $$L=20$$ meters. Take the acceleration due to gravity $$g = 10m{s^{ - 2}}$$ and the velocity of sound is $$300$$ $$m{s^{ - 1}}$$. Then the fractional error in the measurement, $$\delta L/L,$$ is closest to
6
A rocket is launched normal to the surface of the Earth, away from the sun, along the line joining the Sun and the Earth. The Sun is $$3 \times 10{}^5$$ times heavier than the earth and is at a distance $$2.5 \times {10^4}$$ times larger than the radius of the Earth. The escape velocity from Earth's gravitational field is $${V_c} = 11.2km\,{s^{ - 1}}.$$. The minimum initial velocity $$\left( {{v_s}} \right)$$ required for the rocket to be able to leave the sun-earth system is closest to (Ignore the the rotation and revoluation of the earth and the presence of any other planet)
7
Three vectors $$\overrightarrow P ,\overrightarrow Q $$ and $$\overrightarrow R $$ are shown in the figure. Let $$S$$ be any point on the vector $$\overrightarrow R .$$ The distance between the points $$P$$ and $$S$$ is $$b\left| {\overrightarrow R } \right|.$$ The general relation among vectors $$\overrightarrow P ,\overrightarrow Q $$ and $$\overrightarrow S $$ is :


8
A symmetric star shaped conducting wire loop is carrying a steady state current $${\rm I}$$ as shown in the figure. The distance between the diametrically opposite vertices of the star is $$4a.$$ The magnitude of the magnetic field at the center of the loop is
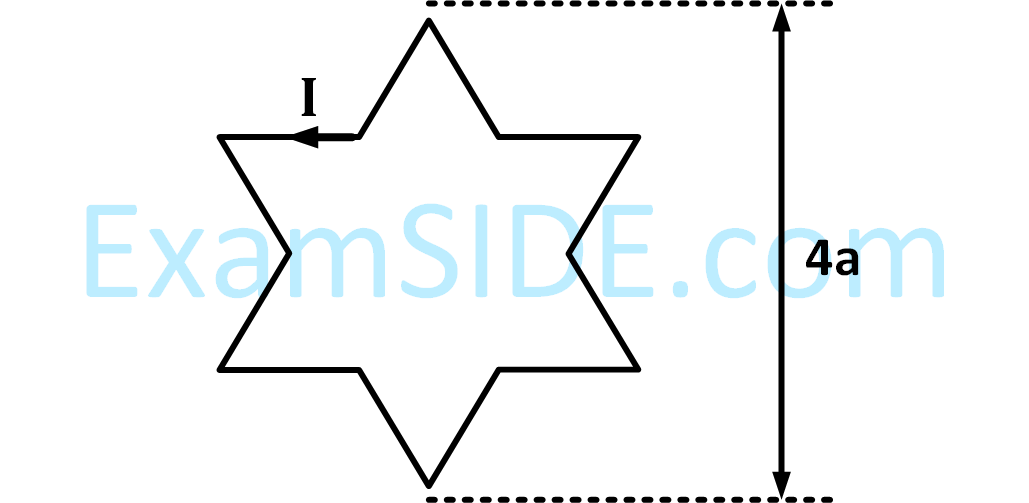

9
A photoelectric material having work-function $${\phi _0}$$ is illuminated with light of wavelength $$\lambda \left( {\lambda < {{he} \over {{\phi _0}}}} \right).$$ The fastest photoelectron has a de-Broglic wavelength $${\lambda _d}.$$ A change in wavelength of the incident light by $$\Delta \lambda $$ result in a change $$\Delta {\lambda _d}$$ in $${\lambda _d}.$$ Then the ratio $$\Delta {\lambda _d}/\Delta \lambda $$ is proportional to
10
Consider regular polygons with number of sides $$n=3,4,5....$$ as shown in the figure. The center of mass of all the polygons is at height $$h$$ from the ground. They roll on a horizontal surface about the leading vertex without slipping and sliding as depicted. The maximum increase in height of the locus of the center of mass for each polygon is $$\Delta $$. Then $$\Delta $$ depends on $$n$$ and $$h$$ as
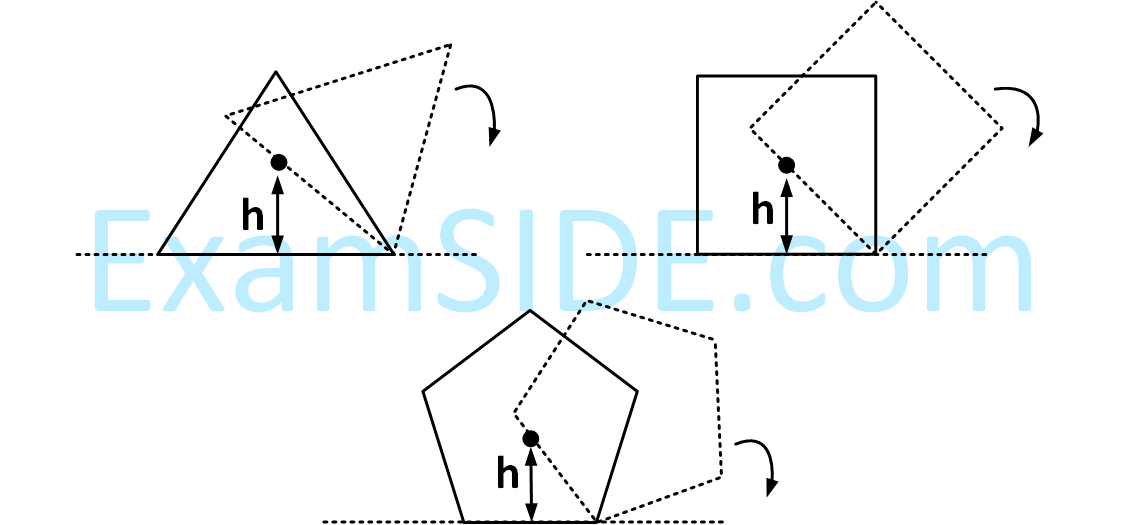

11
Consider an expanding sphere of instantaneous radius R whose total mass remains constant. The expansion is such that the instantaneous density $$\rho $$ remains uniform throughout the volume. The rate of fractional change in density $$\left( {{1 \over \rho } {{d\rho } \over {dt}}} \right)$$ is constant. The velocity $$v$$ of any point on the surface of the expanding sphere is proportional to
12
A wheel of radius R and mass M is placed at the bottom of a fixed step of height R as shown in the figure. A constant force is continuously applied on the surface of the wheel so that it just climbs the step without slipping. Consider the torque $$\tau$$ about an axis normal to the plane of the paper passing through the point Q. Which of the following options is/are correct?


13
A rigid uniform bar AB of length L is slipping from its vertical position on a frictionless floor (as shown in the figure). At some instant of time, the angle made by the bar with the vertical is $$\theta$$. Which of the following statements about its motion is/are correct?


14
A source of constant voltage V is connected to a resistance R and two ideal inductors L1 and L2 through a switch S as shown. There is no mutual inductance between the two inductors. The switch S is initially open. At t = 0, the switch is closed and current begins to flow. Which of the following options is/are correct?


15
In Process 1, the energy stored in the capacitor EC and heat dissipated across resistance ED are related by
16
In Process 2, total energy dissipated across the resistance ED is
17
The total kinetic energy of the ring is
18
The minimum value of $$\omega$$0 below which the ring will drop down is