A person measures the depth of a well by measuring the time interval between dropping a stone and receiving the sound of impact with the bottom of the well. The error in his measurement of time is $$\delta T = 0.01$$ seconds and he measures the depth of the well to be $$L=20$$ meters. Take the acceleration due to gravity $$g = 10m{s^{ - 2}}$$ and the velocity of sound is $$300$$ $$m{s^{ - 1}}$$. Then the fractional error in the measurement, $$\delta L/L,$$ is closest to

A rocket is launched normal to the surface of the Earth, away from the sun, along the line joining the Sun and the Earth. The Sun is $$3 \times 10{}^5$$ times heavier than the earth and is at a distance $$2.5 \times {10^4}$$ times larger than the radius of the Earth. The escape velocity from Earth's gravitational field is $${V_c} = 11.2km\,{s^{ - 1}}.$$. The minimum initial velocity $$\left( {{v_s}} \right)$$ required for the rocket to be able to leave the sun-earth system is closest to (Ignore the the rotation and revoluation of the earth and the presence of any other planet)

Three vectors $$\overrightarrow P ,\overrightarrow Q $$ and $$\overrightarrow R $$ are shown in the figure. Let $$S$$ be any point on the vector $$\overrightarrow R .$$ The distance between the points $$P$$ and $$S$$ is $$b\left| {\overrightarrow R } \right|.$$ The general relation among vectors $$\overrightarrow P ,\overrightarrow Q $$ and $$\overrightarrow S $$ is :

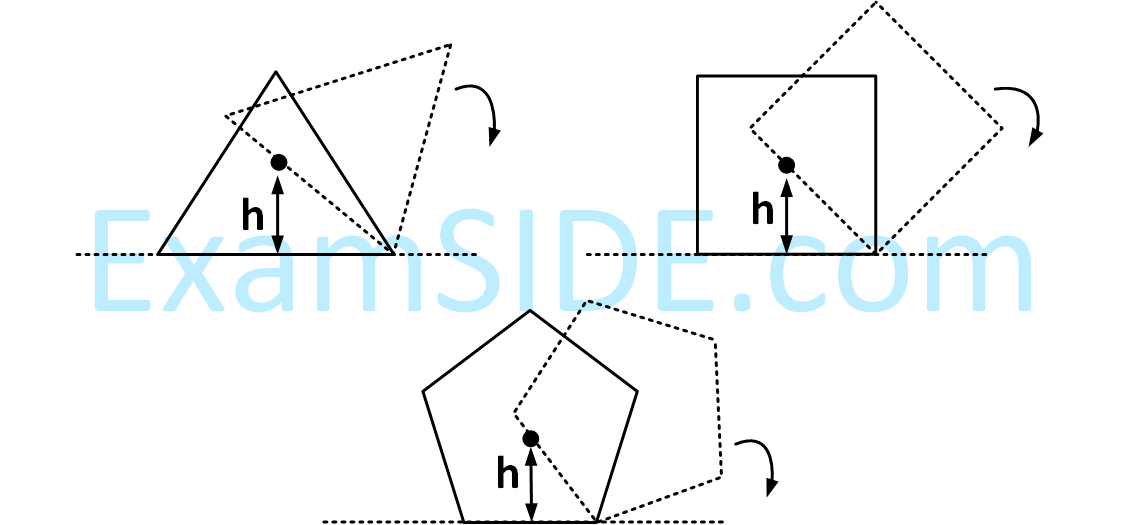
Consider regular polygons with number of sides $$n=3,4,5....$$ as shown in the figure. The center of mass of all the polygons is at height $$h$$ from the ground. They roll on a horizontal surface about the leading vertex without slipping and sliding as depicted. The maximum increase in height of the locus of the center of mass for each polygon is $$\Delta $$. Then $$\Delta $$ depends on $$n$$ and $$h$$ as