1
GATE ECE 2008
MCQ (Single Correct Answer)
+2
-0.6
A two-port network shown below is excited by external dc sources. The voltages and the currents are measured with voltmeters $${V_1}$$, $${V_2}$$ and ammeter $${A_1}$$, $${A_2}$$ (all assumed to be ideal), as indicated. Under following switch conditions, the readings obtained are:
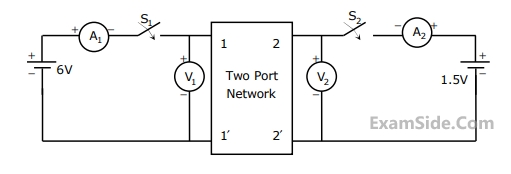 The h-parameter matrix for this network is
The h-parameter matrix for this network is
(i) $${S_1} - open,\,\,\,\,{S_2} - closed$$
$${A_1} = 0\,A,\,\,\,\,\,\,{V_1} = \,4.5\,\,V,$$
$${V_2}\, = \,1.5\,V,\,\,\,\,{A_2}\, = \,1\,A$$
(ii) $${S_1} - Closed,\,\,\,\,{S_2} - Open$$
$${A_1} = 4\,A,\,\,\,\,\,\,{V_1} = \,6\,\,V,$$
$${V_2}\, = \,6\,V,\,\,\,\,{A_2}\, = \,0\,A$$
 The h-parameter matrix for this network is
The h-parameter matrix for this network is 2
GATE ECE 2008
MCQ (Single Correct Answer)
+1
-0.3
In the following graph, the number of trees (P) and the number of cut-sets (Q)
are
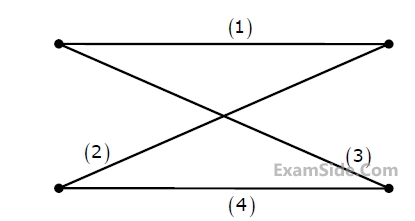

3
GATE ECE 2008
MCQ (Single Correct Answer)
+2
-0.6
The circuit shown in the figure is used to charge the capacitor C alternately from two current sources as indicated. The switches S1 and S2 are mechanically coupled and connected as follows

Assume that the capacitor has zero initial charge. Given that u(t) is a unit step function, the voltage Vc(t) across the capacitor is given by
4
GATE ECE 2008
MCQ (Single Correct Answer)
+2
-0.6
The following series RLC circuit with zero initial conditions is excited by a unit
impulse function $$\delta$$(t).
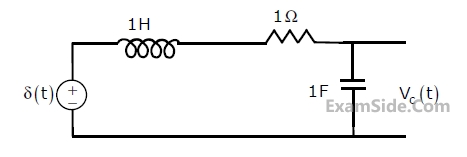 For t > 0, the voltage across the resistor is
For t > 0, the voltage across the resistor is
 For t > 0, the voltage across the resistor is
For t > 0, the voltage across the resistor isPaper analysis
Total Questions
Analog Circuits
5
Communications
9
Control Systems
11
Digital Circuits
6
Electromagnetics
6
Electronic Devices and VLSI
8
Engineering Mathematics
11
Microprocessors
1
Network Theory
9
Signals and Systems
9
More papers of GATE ECE
GATE ECE 2025
GATE ECE 2024
GATE ECE 2023
GATE ECE 2022
GATE ECE 2021
GATE ECE 2019
GATE ECE 2018
GATE ECE 2017 Set 2
GATE ECE 2017 Set 1
GATE ECE 2016 Set 3
GATE ECE 2016 Set 2
GATE ECE 2016 Set 1
GATE ECE 2015 Set 2
GATE ECE 2015 Set 3
GATE ECE 2015 Set 1
GATE ECE 2014 Set 1
GATE ECE 2014 Set 4
GATE ECE 2014 Set 3
GATE ECE 2014 Set 2
GATE ECE 2013
GATE ECE 2012
GATE ECE 2011
GATE ECE 2010
GATE ECE 2009
GATE ECE 2008
GATE ECE 2007
GATE ECE 2006
GATE ECE 2005
GATE ECE 2004
GATE ECE 2003
GATE ECE 2002
GATE ECE 2001
GATE ECE 2000
GATE ECE 1999
GATE ECE 1998
GATE ECE 1997
GATE ECE 1996
GATE ECE 1995
GATE ECE 1994
GATE ECE 1993
GATE ECE 1992
GATE ECE 1991
GATE ECE 1990
GATE ECE 1989
GATE ECE 1988
GATE ECE 1987
GATE ECE
Papers
2025
2024
2023
2022
2021
2019
2018
2014
2013
2012
2011
2010
2009
2008
2007
2006
2005
2004
2003
2002
2001
2000
1999
1998
1997
1996
1995
1994
1993
1992
1991
1990
1989
1988
1987



