The impulse response h(t) of a linear time-invariant continuous time system is described by $$h\left( t \right) = \,\,\exp \left( {\alpha t} \right)u\left( t \right)\,\,\, + \,\,\exp \left( {\beta t} \right)u\left( { - t} \right),$$ where u(t) denotes the unit step function, and $$\alpha $$ and $$\beta $$ are real constants. This system is stable if

In the following network (Fig.1), the switch is closed at t = 0 and the sampling starts from t=0. The sampling frequency is 10 Hz.

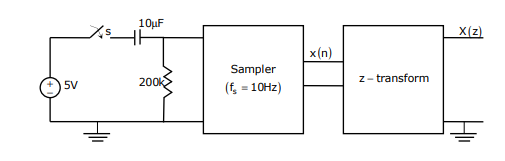
The samples x (n) (n=0, 1, 2,...........) are given by

In the following network (Fig .1), the switch is closed at t = 0- and the sampling starts from t = 0. The sampling frequency is 10 Hz.
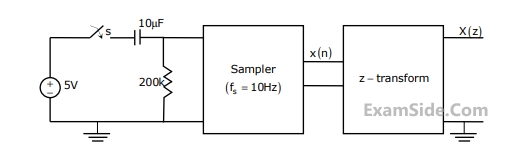
The expression and the region of convergence of the z-transform of the sampled signal are

{x(n)} is a real-valued periodic sequence with a period N. x(n) and X(k) form N-point. Discrete Fourier Transform (DFT) pairs. The DFT Y(k) of the sequence
y (n) = $${1 \over N}\,\sum\limits_{r = 0}^{N - 1} x \,\left( r \right)x\,(n + r\,)$$ is