The entropy versus temperature plot for phases $\alpha$ and $\beta$ at 1 bar pressure is given. $S_{\mathrm{T}}$ and $S_0$ are entropies of the phases at temperatures $\mathrm{T}$ and $0 \mathrm{~K}$, respectively.


The transition temperature for $\alpha$ to $\beta$ phase change is $600 \mathrm{~K}$ and $C_{\mathrm{p}, \beta}-C_{\mathrm{p}, \alpha}=1 \mathrm{~J} \mathrm{~mol}^{-1} \mathrm{~K}^{-1}$. Assume $\left(C_{\mathrm{p}, \beta}-C_{\mathrm{p}, \alpha}\right)$ is independent of temperature in the range of 200 to $700 \mathrm{~K} . C_{\mathrm{p}, \alpha}$ and $C_{\mathrm{p}, \beta}$ are heat capacities of $\alpha$ and $\beta$ phases, respectively.

The value of entropy change, $S_\beta-S_\alpha$ (in $\mathrm{J} \mathrm{mol}^{-1} \mathrm{~K}^{-1}$ ), at $300 \mathrm{~K}$ is _______.

[Use : $\ln 2=0.69$

Given : $S_\beta-S_\alpha=0$ at $0 \mathrm{~K}$ ]

The entropy versus temperature plot for phases $\alpha$ and $\beta$ at 1 bar pressure is given. $S_{\mathrm{T}}$ and $S_0$ are entropies of the phases at temperatures $\mathrm{T}$ and $0 \mathrm{~K}$, respectively.


The transition temperature for $\alpha$ to $\beta$ phase change is $600 \mathrm{~K}$ and $C_{\mathrm{p}, \beta}-C_{\mathrm{p}, \alpha}=1 \mathrm{~J} \mathrm{~mol}^{-1} \mathrm{~K}^{-1}$. Assume $\left(C_{\mathrm{p}, \beta}-C_{\mathrm{p}, \alpha}\right)$ is independent of temperature in the range of 200 to $700 \mathrm{~K} . C_{\mathrm{p}, \alpha}$ and $C_{\mathrm{p}, \beta}$ are heat capacities of $\alpha$ and $\beta$ phases, respectively.

$$ \text { The value of enthalpy change, } \mathrm{H}_\beta-\mathrm{H}_\alpha \text { (in } \mathrm{J} \mathrm{mol}^{-1} \text { ), at } 300 \mathrm{~K} \text { is } $$ ________.

One mole of an ideal monoatomic gas undergoes two reversible processes $(\mathrm{A} \rightarrow \mathrm{B}$ and $\mathrm{B} \rightarrow \mathrm{C})$ as shown in the given figure:


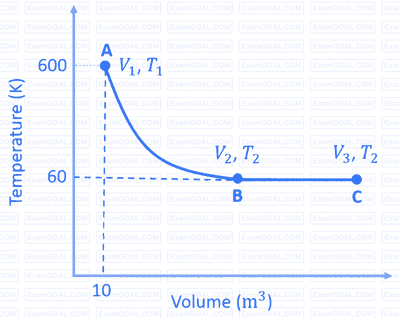
$\mathrm{A} \rightarrow \mathrm{B}$ is an adiabatic process. If the total heat absorbed in the entire process $(\mathrm{A} \rightarrow \mathrm{B}$ and $\mathrm{B} \rightarrow \mathrm{C})$ is $\mathrm{R} T_2 \ln 10$, the value of $2 \log V_3$ is _______.

[Use, molar heat capacity of the gas at constant pressure, $C_{\mathrm{p}, \mathrm{m}}=\frac{5}{2} \mathrm{R}$ ]

In a one-litre flask, 6 moles of $A$ undergoes the reaction $A(\mathrm{~g}) \rightleftharpoons P(\mathrm{~g})$. The progress of product formation at two temperatures (in Kelvin), $\mathrm{T}_1$ and $\mathrm{T}_2$, is shown in the figure:


If $\mathrm{T}_1=2 \mathrm{~T}_2$ and $\left(\Delta \mathrm{G}_2^{\Theta}-\Delta \mathrm{G}_1^{\Theta}\right)=\mathrm{RT}_2 \ln \mathrm{x}$, then the value of $\mathrm{x}$ is _______.

$\left[\Delta \mathrm{G}_1^{\Theta}\right.$ and $\Delta \mathrm{G}_2^{\Theta}$ are standard Gibb's free energy change for the reaction at temperatures $\mathrm{T}_1$ and $\mathrm{T}_2$, respectively.]