One mole of an ideal gas at 900 K, undergoes two reversible processes, I followed by II, as shown below. If the work done by the gas in the two processes are same, the value of $$\ln {{{V_3}} \over {{V_2}}}$$ is _________.


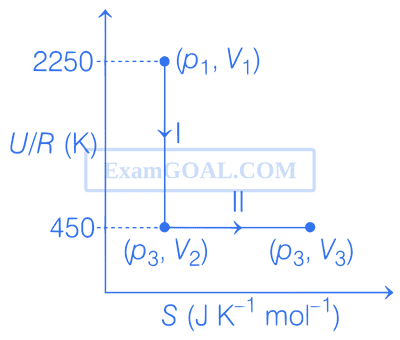
(U : internal energy, S : entropy, p : pressure, V : volume, R : gas constant)

(Given : molar heat capacity at constant volume, C_V,m of the gas is $${5 \over 2}$$R)

For the reaction, X(s) $$\rightleftharpoons$$ Y(s) + Z(g), the plot of $$\ln {{pz} \over {{p^\theta }}}$$ versus $${{{{10}^4}} \over T}$$ is given below (in solid line), where p_z is the pressure (in bar) of the gas Z at temperature T and $${{p^\theta }}$$ = 1 bar.


(Given, $${{d(\ln K)} \over {d\left( {{1 \over T}} \right)}} = - {{\Delta {H^\theta }} \over R}$$, where the equilibrium
constant, $$K = {{pz} \over {{p^\theta }}}$$ and the gas constant, R = 8.314 J K^$$-$$1 mol^$$-$$1)

The value of standard enthalpy, $$\Delta$$H^o (in kJ mol^$$-$$1) for the given reaction is _______.

For the reaction, X(s) $$\rightleftharpoons$$ Y(s) + Z(g), the plot of $$\ln {{pz} \over {{p^\theta }}}$$ versus $${{{{10}^4}} \over T}$$ is given below (in solid line), where p_z is the pressure (in bar) of the gas Z at temperature T and $${{p^\theta }}$$ = 1 bar.


(Given, $${{d(\ln K)} \over {d\left( {{1 \over T}} \right)}} = - {{\Delta {H^\theta }} \over R}$$, where the equilibrium
constant, $$K = {{pz} \over {{p^\theta }}}$$ and the gas constant, R = 8.314 J K^$$-$$1 mol^$$-$$1)

The value of $$\Delta$$S^$$\theta$$ (in J K^$$-$$1 mol^$$-$$1) for the given reaction, at 1000 K is _________.

Tin is obtained from cassiterite by reduction with coke. Use the data given below to determine the minimum temperature (in K) at which the reduction of cassiterite by coke would take place.

At $$298K:{\Delta _f}H^\circ [Sn{O_2}(s)] = - 581.0$$ mol^-1,

$$\eqalign{ & {\Delta _f}H^\circ [(C{O_2})(g)] = - 394.0\,kJ\,mol{ ^{-1}} \cr & S^\circ [Sn{O_2}(s)] = 56.0J\,{K^{ - 1}}mo{l^{ - 1}} \cr & S^\circ [Sn(s)] = 52.0\,J\,K{ ^{-1}}mo{l^{ - 1}} \cr & S^\circ [C(s)] = 6.0\,J\,{K^{ - 1}}mo{l^{ - 1}} \cr & S^\circ [C{O_2}(g)] = 210.0\,J\,{K^{ - 1}}mo{l^{ - 1}} \cr} $$

Assume that, the enthalpies and the entropies are temperature independent.