In a one-litre flask, 6 moles of $A$ undergoes the reaction $A(\mathrm{~g}) \rightleftharpoons P(\mathrm{~g})$. The progress of product formation at two temperatures (in Kelvin), $\mathrm{T}_1$ and $\mathrm{T}_2$, is shown in the figure:


If $\mathrm{T}_1=2 \mathrm{~T}_2$ and $\left(\Delta \mathrm{G}_2^{\Theta}-\Delta \mathrm{G}_1^{\Theta}\right)=\mathrm{RT}_2 \ln \mathrm{x}$, then the value of $\mathrm{x}$ is _______.

$\left[\Delta \mathrm{G}_1^{\Theta}\right.$ and $\Delta \mathrm{G}_2^{\Theta}$ are standard Gibb's free energy change for the reaction at temperatures $\mathrm{T}_1$ and $\mathrm{T}_2$, respectively.]

$2 \mathrm{~mol} \,\mathrm{of}\, \mathrm{Hg}(\mathrm{g})$ is combusted in a fixed volume bomb calorimeter with excess of $\mathrm{O}_{2}$ at $298 \mathrm{~K}$ and 1 atm into $\mathrm{HgO}(s)$. During the reaction, temperature increases from $298.0 \mathrm{~K}$ to $312.8 \mathrm{~K}$. If heat capacity of the bomb calorimeter and enthalpy of formation of $\mathrm{Hg}(g)$ are $20.00 \mathrm{~kJ} \mathrm{~K}^{-1}$ and $61.32 \mathrm{~kJ}$ $\mathrm{mol}^{-1}$ at $298 \mathrm{~K}$, respectively, the calculated standard molar enthalpy of formation of $\mathrm{HgO}(s)$ at 298 $\mathrm{K}$ is $\mathrm{X}\, \mathrm{kJ}\, \mathrm{mol}^{-1}$. The value of $|\mathrm{X}|$ is _________ .

[Given: Gas constant $\mathrm{R}=8.3 \mathrm{~J} \mathrm{~K}^{-1} \mathrm{~mol}^{-1}$ ]

One mole of an ideal gas at 900 K, undergoes two reversible processes, I followed by II, as shown below. If the work done by the gas in the two processes are same, the value of $$\ln {{{V_3}} \over {{V_2}}}$$ is _________.


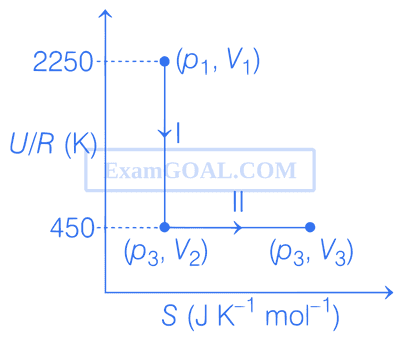
(U : internal energy, S : entropy, p : pressure, V : volume, R : gas constant)

(Given : molar heat capacity at constant volume, C_V,m of the gas is $${5 \over 2}$$R)

For the reaction, X(s) $$\rightleftharpoons$$ Y(s) + Z(g), the plot of $$\ln {{pz} \over {{p^\theta }}}$$ versus $${{{{10}^4}} \over T}$$ is given below (in solid line), where p_z is the pressure (in bar) of the gas Z at temperature T and $${{p^\theta }}$$ = 1 bar.


(Given, $${{d(\ln K)} \over {d\left( {{1 \over T}} \right)}} = - {{\Delta {H^\theta }} \over R}$$, where the equilibrium
constant, $$K = {{pz} \over {{p^\theta }}}$$ and the gas constant, R = 8.314 J K^$$-$$1 mol^$$-$$1)

The value of standard enthalpy, $$\Delta$$H^o (in kJ mol^$$-$$1) for the given reaction is _______.