1
JEE Advanced 2020 Paper 2 Offline
Numerical
+3
-1

A hot air balloon is carrying some passengers, and a few sandbags of mass 1 kg each so that its total
mass is 480 kg. Its effective volume giving the balloon its buoyancy is V. The balloon is floating at
an equilibrium height of 100 m. When N number of sandbags are thrown out, the balloon rises to a
new equilibrium height close to 150 m with its volume V remaining unchanged. If the variation of
the density of air with height h from the ground is
$$\rho \left( h \right) = {\rho _0}{e^{ - {h \over {{h_0}}}}}$$, where $$\rho $$0 = 1.25 kg m−3 and h0 = 6000 m, the value of N is _________.
$$\rho \left( h \right) = {\rho _0}{e^{ - {h \over {{h_0}}}}}$$, where $$\rho $$0 = 1.25 kg m−3 and h0 = 6000 m, the value of N is _________.
Your input ____
2
JEE Advanced 2020 Paper 2 Offline
Numerical
+3
-1

A train with cross-sectional area St
is moving with speed vt
inside a long tunnel of cross-sectional
area S0 (S0 = 4St). Assume that almost all the air (density $$\rho $$) in front of the train flows back between
its sides and the walls of the tunnel. Also, the air flow with respect to the train is steady and laminar.
Take the ambient pressure and that inside the train to be p0. If the pressure in the region between the
sides of the train and the tunnel walls is p, then
p0 - p = $${7 \over {2N}}\rho v_t^2$$. The value of 𝑁 is ________.
p0 - p = $${7 \over {2N}}\rho v_t^2$$. The value of 𝑁 is ________.
Your input ____
3
JEE Advanced 2020 Paper 2 Offline
Numerical
+4
-0

A cubical solid aluminium (bulk modulus = $$ - V{{dP} \over {dV}} = 70GPa$$) block has an edge length of 1 m on the surface of the earth. It is kept on the floor of a 5 km deep ocean. Taking the average density of water and the acceleration due to gravity to be 103 kg m-3 and 10 ms-2, respectively, the change in the edge length of the block in mm is _______.
Your input ____
4
JEE Advanced 2020 Paper 1 Offline
Numerical
+4
-0

When water is filled carefully in a glass, one can fill it to a height h above the rim of the glass due to
the surface tension of water. To calculate h just before water starts flowing, model the shape of the
water above the rim as a disc of thickness h having semicircular edges, as shown schematically in the
figure. When the pressure of water at the bottom of this disc exceeds what can be withstood due to
the surface tension, the water surface breaks near the rim and water starts flowing from there. If the
density of water, its surface tension and the acceleration
due to gravity are 103 kg m−3 , 0.07 Nm−1 and 10 ms−2 , respectively, the value of h (in mm) is _________.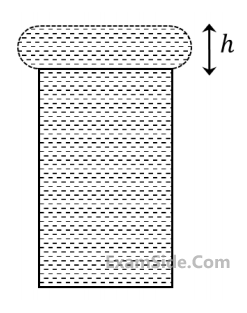
due to gravity are 103 kg m−3 , 0.07 Nm−1 and 10 ms−2 , respectively, the value of h (in mm) is _________.

Your input ____
Questions Asked from Properties of Matter (Numerical)
Number in Brackets after Paper Indicates No. of Questions
JEE Advanced 2024 Paper 1 Online (1)
JEE Advanced 2023 Paper 2 Online (1)
JEE Advanced 2020 Paper 2 Offline (3)
JEE Advanced 2020 Paper 1 Offline (1)
JEE Advanced 2019 Paper 1 Offline (2)
JEE Advanced 2018 Paper 1 Offline (1)
JEE Advanced 2017 Paper 1 Offline (1)
JEE Advanced 2016 Paper 1 Offline (1)
IIT-JEE 2009 Paper 2 Offline (2)
JEE Advanced Subjects
Physics
Mechanics
Units & Measurements Motion Laws of Motion Work Power & Energy Impulse & Momentum Rotational Motion Properties of Matter Heat and Thermodynamics Simple Harmonic Motion Waves Gravitation
Electricity
Electrostatics Current Electricity Capacitor Magnetism Electromagnetic Induction Alternating Current Electromagnetic Waves
Optics
Modern Physics
Chemistry
Physical Chemistry
Some Basic Concepts of Chemistry Structure of Atom Redox Reactions Gaseous State Chemical Equilibrium Ionic Equilibrium Solutions Thermodynamics Chemical Kinetics and Nuclear Chemistry Electrochemistry Solid State Surface Chemistry
Inorganic Chemistry
Periodic Table & Periodicity Chemical Bonding & Molecular Structure Isolation of Elements Hydrogen s-Block Elements p-Block Elements d and f Block Elements Coordination Compounds Salt Analysis
Organic Chemistry
Mathematics
Algebra
Quadratic Equation and Inequalities Sequences and Series Mathematical Induction and Binomial Theorem Matrices and Determinants Permutations and Combinations Probability Vector Algebra 3D Geometry Statistics Complex Numbers
Trigonometry
Coordinate Geometry
Calculus