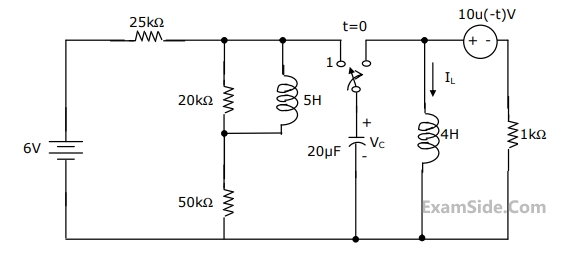
(a) Determine $${V_C}\left( {{0^ + }} \right)$$ and $${I_{_L}}\left( {{0^ + }} \right)$$
(b) Determine $${{d{V_C}\left( t \right)} \over {dt}}\,\,$$ at $$t\, = \,{0^ + }$$
(c) Determine $${{V_C}\left( t \right)}$$ for $$t > 0$$
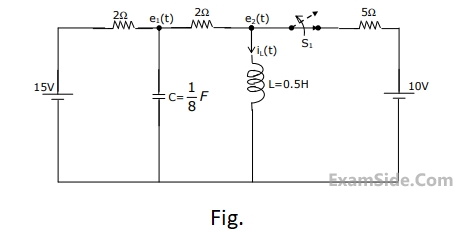
(a) Find $${i_L}\left( {{0^ + }} \right)$$.
(b) Find $${e_1}\left( {{0^ + }} \right)$$.
(c) Using nodal equations and Laplace transform approach, find an expression
for the voltage across the capacitor for all $$t\, = \,0$$.
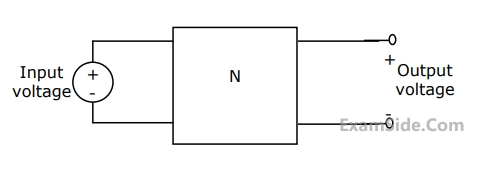
(a) Find the voltage transfer function of the network.
(b) Find L, and draw the configuration of the network.
(c) Find the impulse response of the network.
 n
n
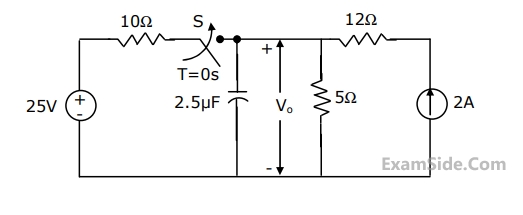
(a) Find $${V_0}$$ for $$t \le 0$$ and as $$t \to \infty $$.
(b) Write an expression for $${V_0}$$ as a function of time for $$0 \le t \le \infty $$.
(c) Evaluate $${V_0}$$ at $$t = 25\,\,\mu $$sec.