1
GATE ECE 2008
MCQ (Single Correct Answer)
+2
-0.6
The driving point impedance of the following network is given by $$Z(s) = {{0.2\,s} \over {{s^2}\, + \,0.1\,s\, + \,2}}$$. The component values are
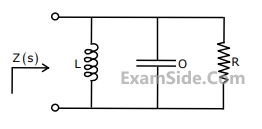

2
GATE ECE 2006
MCQ (Single Correct Answer)
+2
-0.6
A two-port network is represented by ABCD parameters given by
$$\left[ {\matrix{
{{V_1}} \cr
{{I_1}} \cr
} } \right] = \,\left[ {\matrix{
A & B \cr
C & D \cr
} } \right]\,\left[ {\matrix{
{{V_2}} \cr
{ - \,{I_2}} \cr
} } \right]$$
If port-2 is terminated by $${R_L}$$, the input impedance seen at port-1 is given by
3
GATE ECE 2006
MCQ (Single Correct Answer)
+2
-0.6
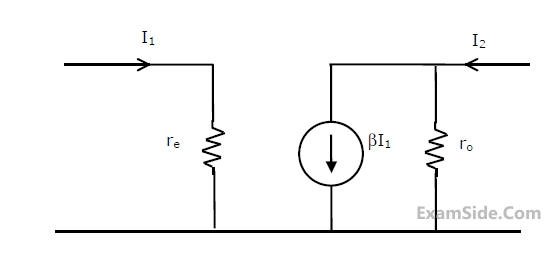
In the two port network shown in the figure below, z12 and z21 are, respectively

4
GATE ECE 2005
MCQ (Single Correct Answer)
+2
-0.6
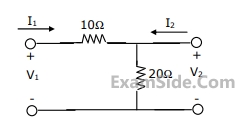
The h parameters of the circuit shown in Fig. are

Questions Asked from Two Port Networks (Marks 2)
Number in Brackets after Paper Indicates No. of Questions
GATE ECE 2025 (1)
GATE ECE 2024 (1)
GATE ECE 2023 (2)
GATE ECE 2022 (1)
GATE ECE 2016 Set 3 (1)
GATE ECE 2015 Set 3 (1)
GATE ECE 2014 Set 4 (2)
GATE ECE 2014 Set 2 (1)
GATE ECE 2011 (1)
GATE ECE 2008 (3)
GATE ECE 2006 (2)
GATE ECE 2005 (2)
GATE ECE 2004 (2)
GATE ECE 2003 (2)
GATE ECE 2001 (1)
GATE ECE 1999 (1)
GATE ECE 1997 (1)
GATE ECE 1995 (1)
GATE ECE 1992 (1)
GATE ECE 1991 (1)
GATE ECE 1989 (3)
GATE ECE 1988 (1)
GATE ECE Subjects
Signals and Systems
Representation of Continuous Time Signal Fourier Series Discrete Time Signal Fourier Series Fourier Transform Discrete Time Signal Z Transform Continuous Time Linear Invariant System Transmission of Signal Through Continuous Time LTI Systems Discrete Time Linear Time Invariant Systems Sampling Continuous Time Signal Laplace Transform Discrete Fourier Transform and Fast Fourier Transform Transmission of Signal Through Discrete Time Lti Systems Miscellaneous Fourier Transform
Network Theory
Control Systems
Digital Circuits
General Aptitude
Electronic Devices and VLSI
Analog Circuits
Engineering Mathematics
Microprocessors
Communications
Electromagnetics