1
GATE ECE 2018
Numerical
+1
-0
The ABCD matrix for a two-port network is defined by :
$$\left[ {\matrix{ {{V_1}} \cr {{I_1}} \cr } } \right] = \left[ {\matrix{ A & B \cr C & D \cr } } \right]\left[ {\matrix{ {{V_2}} \cr { - {I_2}} \cr } } \right]$$
The parameter B for the given two-port network (in ohms, correct to two decimal places) is _______.
$$\left[ {\matrix{ {{V_1}} \cr {{I_1}} \cr } } \right] = \left[ {\matrix{ A & B \cr C & D \cr } } \right]\left[ {\matrix{ {{V_2}} \cr { - {I_2}} \cr } } \right]$$

The parameter B for the given two-port network (in ohms, correct to two decimal places) is _______.
Your input ____
2
GATE ECE 2016 Set 1
MCQ (Single Correct Answer)
+1
-0.3
Consider a two-port network with the transmission matrix: T = $$\begin{bmatrix}A&B\\C&D\end{bmatrix}$$. If the network is
reciprocal, then
3
GATE ECE 2016 Set 3
Numerical
+1
-0
The z-parameter matrix for the two-port network shown is $$$\left[ {\matrix{
{2\,j\,\omega } & {j\,\omega } \cr
{j\,\omega } & {3\, + \,2\,j\,\omega } \cr
} } \right]$$$
Where the entries are in $$\Omega $$. Suppose $$\,{Z_b}\,\left( {j\,\omega } \right) = {R_b} + j\,\omega $$
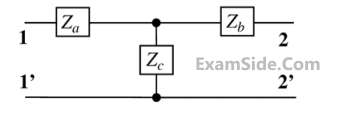 Then the value of $${R_b}$$ (in $$\Omega $$) equals _______________________3
Then the value of $${R_b}$$ (in $$\Omega $$) equals _______________________3
 Then the value of $${R_b}$$ (in $$\Omega $$) equals _______________________3
Then the value of $${R_b}$$ (in $$\Omega $$) equals _______________________3Your input ____
4
GATE ECE 2015 Set 2
MCQ (Single Correct Answer)
+1
-0.3
The 2-port admittance matrix of the circuit shown is given by
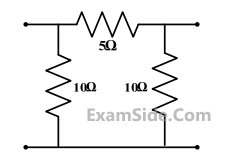

Questions Asked from Two Port Networks (Marks 1)
Number in Brackets after Paper Indicates No. of Questions
GATE ECE Subjects
Signals and Systems
Representation of Continuous Time Signal Fourier Series Discrete Time Signal Fourier Series Fourier Transform Discrete Time Signal Z Transform Continuous Time Linear Invariant System Transmission of Signal Through Continuous Time LTI Systems Discrete Time Linear Time Invariant Systems Sampling Continuous Time Signal Laplace Transform Discrete Fourier Transform and Fast Fourier Transform Transmission of Signal Through Discrete Time Lti Systems Miscellaneous Fourier Transform
Network Theory
Control Systems
Digital Circuits
General Aptitude
Electronic Devices and VLSI
Analog Circuits
Engineering Mathematics
Microprocessors
Communications
Electromagnetics