The frequency of occurrence of 8 symbols (a-h) is shown in the table below. A symbol is chosen and it is determined by asking a series of "yes/no" questions which are assumed to be truthfully answered. The average number of questions when asked in the most efficient sequence, to determine the chosen symbol, is _____________ (rounded off to two decimal places).
| Symbols | a | b | c | d | e | f | g | h |
|---|---|---|---|---|---|---|---|---|
| Frequency of occurrence | $$\frac{1}{2}$$ | $${1 \over 4}$$ | $${1 \over 8}$$ | $${1 \over {16}}$$ | $${1 \over {32}}$$ | $${1 \over {64}}$$ | $${1 \over {128}}$$ | $${1 \over {128}}$$ |
The transition diagram of a discrete memoryless channel with three input symbols and three output symbols is shown in the figure. The transition probabilities are as marked. The parameter $$\alpha$$ lies in the interval [0.25, 1]. The value of .. for which the capacity of this channel is maximized, is __________ (rounded off to two decimal places).
Consider communication over a memoryless binary symmetric channel using a (7, 4) Hamming code. Each transmitted bit is received correctly with probability (1 $$-$$ $$\in$$), and flipped with probability $$\in$$. For each codeword transmission, the receiver performs minimum Hamming distance decoding, and correctly decodes the message bits if and only if the channel introduces at most one bit error. For $$\in$$ = 0.1, the probability that a transmitted codeword is decoded correctly is __________ (rounded off to two decimal places).
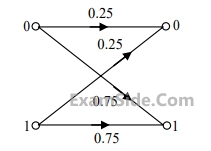The channel is