Consider a binary memoryless channel characterized by the transition probability diagram shown in the figure. 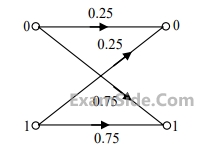The channel is

A binary communication system makes use of the symbols “zero” and “one”. There are channel errors. Consider the following events:
$${x_0}$$ : a " zero " is transmitted
$${x_1}$$ : a " one " is transmitted
$${y_0}$$ : a " zero " is received
$${y_1}$$ : a " one " is received

The following probabilities are given:
$$P({x_0}) = \,{3 \over 4},\,\left( {\,\left. {{y_0}} \right|{x_0}} \right) = \,{1 \over 2},\,\,and\,P\,\,\left( {\,\left. {{y_0}} \right|{x_1}} \right) = \,{1 \over 2}$$.
The information in bits that you obtain when you learn which symbol has been received (while you know that a " zero " has been transmitted) is _____________

Consider a discreet memoryless source with alphabet $$S = \left\{ {{s_0},\,{s_1},\,{s_2},\,{s_3},\,{s_{4......}}} \right\}$$ and respective probabilities of occurrence $$P = \left\{ {{1 \over 2},\,{1 \over 4},\,{1 \over 8},\,{1 \over {16}},\,{1 \over {32}},......} \right\}$$. The entropy of the source (in bits) is__________.

A voice-grade AWGN (additive white Gaussian noise) telephone channel has a bandwidth of 4.0 kHz and two-sided noise power spectral density $${\eta \over 2} = 2.5\, \times \,{10^{ - 5}}$$ Watt per Hz. If information at the rate of 52 kbps is to be transmitted over this channel with arbitrarily small bit error rate, then the minimum bit energy $${E_b}$$ (in mJ/bit) necessary is ________________