Consider communication over a memoryless binary symmetric channel using a (7, 4) Hamming code. Each transmitted bit is received correctly with probability (1 $$-$$ $$\in$$), and flipped with probability $$\in$$. For each codeword transmission, the receiver performs minimum Hamming distance decoding, and correctly decodes the message bits if and only if the channel introduces at most one bit error. For $$\in$$ = 0.1, the probability that a transmitted codeword is decoded correctly is __________ (rounded off to two decimal places).
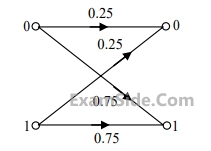The channel is$${x_0}$$ : a " zero " is transmitted
$${x_1}$$ : a " one " is transmitted
$${y_0}$$ : a " zero " is received
$${y_1}$$ : a " one " is received
The following probabilities are given:
$$P({x_0}) = \,{3 \over 4},\,\left( {\,\left. {{y_0}} \right|{x_0}} \right) = \,{1 \over 2},\,\,and\,P\,\,\left( {\,\left. {{y_0}} \right|{x_1}} \right) = \,{1 \over 2}$$.
The information in bits that you obtain when you learn which symbol has been received (while you know that a " zero " has been transmitted) is _____________