Find the Y-parameters (short ciruit admittance parameters) for the network shown in figure.

Consider the network in Fig.

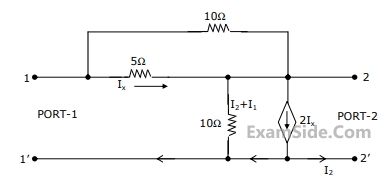
(a) Find its short-circuit admittance parameters.
(b) Find the open-ciruit impedance $${Z_{22}}$$.

The admittance parameters of a 2-port network shown in Fig. are given by $${Y_{11}} = \,2\,\,mho$$, $${Y_{12}}$$ = - 0.5 mho, $${Y_{21}}$$ = 4.8 mho, $${Y_{22}}$$ = 1 mho. The output port is terminated with a load admittance $${Y_L}$$ = 0.2 mho. Find $${E_2}$$ for each of the following conditions:

(a) $${E_1} = \,10\,\angle \,{0^{ \circ \,}}\,V$$
(b) $${I_1} = \,10\,\angle \,{0^{ \circ \,}}\,A$$
(c) A source $$10\,\angle \,{0^{ \circ \,}}\,V$$ in series with a 0.25 $$\Omega $$ resistor is connected to the input port.

Find the input resistance $${R_{in}}$$ of the infinite section resistive network shown in Fig.