Consider the circuit in the diagram. The $$ \oplus $$ operator represents $$EX$$-$$OR.$$ The $$D$$ flip-flops are initialized to zeros (cleared).

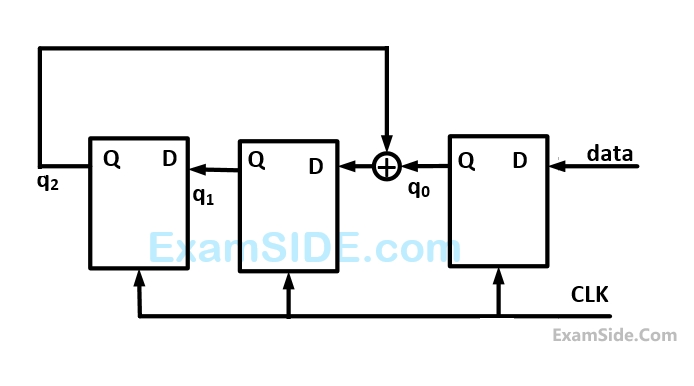
The following data: $$100110000$$ is supplied to the ''data'' terminal in nine clock cycles. After that the values of $${q_2}{q_1}{q_0}$$ are

Consider the partial implementation of a $$2$$-bit counter using $$T$$ flip-flops following the sequence $$0$$-$$2$$-$$3$$-$$1$$-$$0,$$ as shown below.

To complete the circuit, the input $$X$$ should be

A 1- input, 2- output synchronous sequential circuit behaves as follows.

Let $${z_k},\,{n_k}$$ denote the number of $$0’s$$ and $$1’s$$ respectively in initial $$k$$ bits of the input

$$\left({{z_k} + {n_k} = k} \right).$$ The circuit outputs $$00$$ until one of the following conditions holds.

$$ * \,\,\,\,\,$$ $${z_k} = {n_k} + 2.\,\,\,$$ In this case, the output at the $$k$$-th and all subsequent clock ticks is $$10.$$

$$ * \,\,\,\,\,$$ $${n_k} = {z_k} + 2.\,\,\,$$ In this case, the output at the $$k$$-th and all subsequent clock ticks is $$01.$$

What is the minimum number of states required in the state transition graph of the above circuit?

Consider the circuit given below with initial state $${Q_0} = 1,\,\,{Q_1} = {Q_2} = 0.$$ The state of the circuit is given by the value of $$4{Q_2} + 2{Q_1} + {Q_{0.}}$$

Which one of the following is correct state sequence of the circuit?