Functional Dependencies and Normalization · Database Management System · GATE CSE

Marks 1

Which of the following statements about a relation $R$ in first normal form (1NF) is/are TRUE?

GATE CSE 2024 Set 1

In a relational data model, which one of the following statements is TRUE?

GATE CSE 2022

Consider a relation R(A, B, C, D, E) with the following three functional dependencies.

AB $$\to$$ C ; BC $$\to$$ D ; C $$\to$$ E;

The number of superkeys in the relation R is _________.

GATE CSE 2022

Consider the following statements S1 and S2 about the relational data model:

S1: A relation scheme can have at most one foreign key.

S2: A foreign key in a relation scheme R cannot be used to refer to tuples of R.

Which one of the following choices is correct?

GATE CSE 2021 Set 2

A database of research articles in a journal uses the following schema.

(VOLUME, NUMBER, STARTPAGE, ENDPAGE, TITLE, YEAR, PRICE)

The primary key is (VOLUME, NUMBER, STARTPAGE, ENDPAGE) and the following functional dependencies exist in the schema.

(VOLUME, NUMBER, STARTPAGE, ENDPAGE) → TITLE
(VOLUME, NUMBER) → YEAR
(VOLUME, NUMBER, STARTPAGE, ENDPAGE) → PRICE

The database is redesigned to use the following schemas.

(VOLUME, NUMBER, STARTPAGE, ENDPAGE, TITLE, PRICE)
(VOLUME, NUMBER, YEAR)

Which is the weakest normal form that the new database satisfies, but the old one does not?

GATE CSE 2016 Set 1

Consider the relation $$X\left( {P,Q,R,S,T,U} \right)$$ with the following set of functional dependencies
$$\eqalign{ & F = \left\{ \, \right. \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left\{ {P,R} \right\} \to \left\{ {S,T} \right\}, \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left\{ {P,S,U} \right\} \to \left\{ {Q,R} \right\} \cr & \,\,\,\,\,\,\,\,\,\,\left. \, \right\} \cr} $$
Which of the following is the trivial functional dependency in $${F^ + },$$ where $${F^ + }$$ is closure of $$f$$ ?

GATE CSE 2015 Set 3

A prime attribute of a relation scheme $$R$$ is an attribute that appears

GATE CSE 2014 Set 3

Consider the relation schema $$R = \left( {E,\,F,\,G,\,H,\,I,\,J,\,K,L,\,M,\,N} \right)$$ and the set of functional dependencies $$\left\{ {\left\{ {E,F} \right\} \to \left\{ G \right\},\left\{ F \right\}} \right.$$
$$ \to \left\{ {I,J} \right\},\left\{ {E,H} \right\} \to \left\{ {K,L} \right\},\left\{ K \right\}$$
$$ \to \left\{ M \right\},\left\{ L \right\}$$
$$ \to \left. {\left\{ N \right\}} \right\}$$ on $$R.$$ What is the key for $$R?$$

GATE CSE 2014 Set 1

The maximum number of superkeys for the relation schema $$R(E, F, G, H)$$ with $$E$$ as key is ______.

GATE CSE 2014 Set 2

Which of the following is TRUE?

GATE CSE 2012

A table has fields, $$F1, F2, F3, F4, F5,$$ with the following functional dependencies:
$$F1 \to F3.\,F2 \to F4.\,\,\,\left( {F1\,.\,F2} \right) \to F5$$ in terms of Normalization, this table is in

GATE CSE 2005

Which one of the following statements about normal forms is FALSE?

GATE CSE 2005

Relation $$R$$ with an associated set of functional dependencies, $$F,$$ is decomposed into $$BCNF.$$ The redundancy (arising out of functional dependencies) in the resulting set of relations is

GATE CSE 2002

Consider a schema $$R(A,B,C,D)$$ and functional dependencies $$A \to B\,\,$$ and $$C \to D\,\,$$. Then the decomposition of $$R$$ into $${R_1}\left( {AB} \right)$$ and $${R_2}\left( {CD} \right)$$ is

GATE CSE 2001

Let $$R=(A,B,C,D,E,F)$$ be a relation scheme with the following dependencies: $$C \to F,\,E \to A,\,EC \to D,\,A \to B.$$ Which of the following is a key for $$R?$$

GATE CSE 1999

Which normal form is considered adequate for normal relational database design?

GATE CSE 1998

State True or False with reason. There is always a decomposition into Boyce-codd normal form $$(BCNF)$$ that is lossless and dependency preserving.

GATE CSE 1994

Marks 2

Consider the following relational schema along with all the functional dependencies that hold on them.

$$\begin{aligned} & R 1(A, B, C, D, E):\{D \rightarrow E, E A \rightarrow B, E B \rightarrow C\} \\ & R 2(A, B, C, D):\{A \rightarrow D, A \rightarrow B, C \rightarrow A\} \end{aligned}$$

Which of the following statement(s) is/are TRUE?

GATE CSE 2025 Set 2

Consider a relational schema team(name, city, owner), with functional dependencies \{name $\rightarrow$ city, name $\rightarrow$ owner}.

The relation team is decomposed into two relations, $t 1$ (name, city) and $t 2$ (name, owner). Which of the following statement(s) is/are TRUE?

GATE CSE 2025 Set 1

A functional dependency $F: X \to Y$ is termed as a useful functional dependency if and only if it satisfies all the following three conditions:

$X$ is not the empty set.
$Y$ is not the empty set.
Intersection of $X$ and $Y$ is the empty set.

For a relation $R$ with 4 attributes, the total number of possible useful functional dependencies is _________

GATE CSE 2024 Set 2

The symbol → indicates functional dependency in the context of a relational database. Which of the following options is/are TRUE?

GATE CSE 2024 Set 1

Suppose the following functional dependencies hold on a relation U with attributes P, Q, R, S, and T :

P → QR

RS → T

Which of the following functional dependencies can be inferred from the above functional dependencies?

GATE CSE 2021 Set 2

Consider the relation R(P, Q, S, T, X, Y, Z, W) with the following functional dependencies.

PQ → X; P → YX; Q → Y; Y → ZW

Consider the decomposition of the relation R into the constituent relations according to the following two decomposition schemes.

D₁ : R = [(P, Q, S, T); (P, T, X); (Q, Y); (Y, Z, W)]

D₂ : R = [(P, Q, S); (T, X); (Q, Y); (Y, Z, W)]

Which one of the following options is correct?

GATE CSE 2021 Set 1

Consider a relational table R that is in 3NF, but not in BCNF. Which one of the following statements is TRUE?

GATE CSE 2020

Let the set of functional dependencies

F = {QR → S, R → P, S → Q}

hold on a relation schema X = (PQRS). X is not in BCNF. Suppose X is decomposed into two schemas Y and Z, where Y = (PR) and Z = (QRS).

Consider the two statements given below.

I. Both Y and Z are in BCNF
II. Decomposition of X into Y and Z is dependency preserving and lossless

Which of the above statements is/are correct?

GATE CSE 2019

Consider an Entity-Relationship (ER) model in which entity sets E₁ and E₂ are connected by an m : n relationship R₁₂. E₁ and E₃ are connected by a 1 : n (1 on the side of E₁ and n on the side of E₃) relationship R₁₃.

E₁ has two single-valued attributes a₁₁ and a₁₂ of which a₁₁ is the key attribute. E₂ has two single-valued attributes a₂₁ and a₂₂ of which a₂₁ is the key attribute. E₃ has two single-valued attributes a₃₁ and a₃₂ of which a₃₁ is the key attribute. The relationships do not have any attributes.

If a relational model is derived from the above ER model, then the minimum number of relations that would be generated if all the relations are in 3NF is _______.

GATE CSE 2015 Set 1

Given the following two statements:
$$S1:$$ Every table with two single-valued attributes is in $$1NF, 2NF, 3NF$$ and $$BCNF.$$
$$S2:$$ $$AB \to C,\,\,D \to E,\,\,E \to C$$ is a minimal cover for the set of functional dependencies $$AB \to C,$$ $$D \to E,\,\,AB \to E,\,\,E \to C.$$

Which one of the following is CORRECT?

GATE CSE 2014 Set 1

Relation $$R$$ has eight attribution $$ABCDEFGH.$$ Fields of $$R$$ contain only atomic values.
$$F = \left\{ {CH \to G,\,\,A \to BC,\,B \to CFH,\,\,E \to A,\,\,F \to EG} \right\}$$ set of functional dependencies $$(FDs)$$ so that $${F^ + }$$ is exactly the set of $$FDs$$ that hold for $$R.$$

How many candidate keys does the relation $$R$$ have?

GATE CSE 2013

The relation $$R$$ is

GATE CSE 2013

Let $$R\left( {A,\,B,\,C,\,D,E,P,G} \right)$$ be a relational schema in which the following functional dependencies are known to hold: $$AB \to CD,\,\,DE \to P,\,\,C \to E.\,\,P \to C$$ and $$B \to G.$$ The relational schema $$R$$ is

GATE CSE 2008

Let $$R\left( {A,B,C,D} \right)$$ be a relational schema with the following functional dependencies:
$$A \to B,\,\,B \to C,\,\,C \to D$$ and $$D \to B.$$
The decomposition of $$R$$ into $$(A,B), (B,C)$$ and $$(B,D)$$

GATE CSE 2008

Consider the following relational schemes for a library database. Book ( Title, Author, Catalog_ no, Publisher, Year, Pr ice ) Collection ( Title, Author, Catalog no )
With in the following functional dependencies:
$${\rm I}.\,\,\,\,\,\,$$ Title Author $$ \to $$ Catalog_no
$${\rm II}.\,\,\,\,$$ Catalog_no $$ \to $$ Title Author Publisher Year
$${\rm III}.\,\,\,\,$$ Publisher Title Year $$ \to $$ Price

Assume { Author, Title } is the key for both schemes. Which of the following statements is true?

GATE CSE 2008

Which one of the following statements if FALSE?

GATE CSE 2007

Consider the relation enrolled (student, course) in which (student, course ) is the primary key, and the relation Paid (student, amount) where student is the primary key. Assume no null values and no foreign keys or integrity constraints. Assume that amounts $$6000, 7000, 8000,9000$$ and $$10000$$ were each paid by $$20$$% of the students. Consider these query plans (Plan $$1$$ on left, Plan $$2$$ on right) to ''List all courses taken by students who have paid more than $$x''$$.

GATE CSE 2006 Database Management System - Functional Dependencies and Normalization Question 24 English 1

A disk seek takes $$4ms$$, disk data transfer bandwidth is $$300MB/s$$ and checking a tuple to see if amount is greater than $$x$$ takes $$10\mu s.$$ Which of the following statements is correct?

GATE CSE 2006

The following functional dependencies are given :
$$\eqalign{ & AB \to CD,\,AF \to D,\,\,DE \to F, \cr & C \to G.\,\,\,\,\,\,\,\,\,\,F \to E.\,\,\,\,\,\,\,\,\,G \to A. \cr} $$

Which one of the following options is false?

GATE CSE 2006

Consider a relation scheme $$R = \left( {A,\,B,\,C,\,D,\,E,\,H} \right)$$ on which the following functional dependencies hold: $$\left\{ {A \to B,\,\,BC \to D,\,\,E \to C,\,\,D \to A} \right\}.$$ What are the candidate keys of $$R?$$

GATE CSE 2005

In a schema with attributes $$A, B, C, D,$$ and $$E,$$ following set of functional dependencies are given
$$\eqalign{ & \,\,\,A \to B \cr & \,\,\,A \to C \cr & CD \to E \cr & \,\,\,B \to D \cr & \,\,\,E \to A \cr} $$

Which of the following functional dependencies is NOT implied by the above set?

GATE CSE 2005

The relation scheme student Performance (Name, CourseNo, RollNo, Grade) has the following functional dependencies:

Name, courseNo $$\,\, \to \,\,$$ grade
RollNo, courseNo $$\,\, \to \,\,$$ grade
$$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,$$$$\,\,\,\,\,\,\,\,\,$$ Name $$\,\, \to \,\,$$ rollNo
$$\,\,\,\,\,\,\,\,\,\,\,\,\,$$$$\,\,\,\,\,\,\,\,\,$$ RollNo $$\,\, \to \,\,$$ name

The highest normal form of this relation scheme is

GATE CSE 2004

A relation Empdt $$1$$ is defined with attributes empcode (unique), name, street, city, state and pincode. For any pincode, there is only one city and state. Also, for any given street city and the state, there is just one pincode. In normalization terms, Empdt$$1$$ is a relation in

GATE CSE 2004

Consider the following functional dependencies in a database.
$$\eqalign{ & \,\,\,\,Date\,\,of\,\,Birth\,\, \to \,\,Age \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,Age\,\, \to \,\,Eligibility \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,Name\,\, \to \,\,Roll\_number \cr & \,\,\,\,\,Roll\_number\,\, \to \,\,Name \cr & Course\_number\, \to \,\,Course\_name \cr & Course\_number\, \to Instructor \cr & (Roll\_Number,\,Course\_number)\,\, \to \,\,Grade \cr} $$

The relation (Roll_number, Name, Date_of_Birth, Age) is

GATE CSE 2003

From the following instance of a relation schema $$R(A, B, C),$$ we can conclude that:

GATE CSE 2002

Relation $$R$$ is decomposed using a set of functional dependencies, $$F,$$ and relation $$S$$ is decomposed using another set of functional dependencies, $$G.$$ One decomposition is definitely $$BCNF,$$ the other is definitely. $$3NF,$$ but it is not known which is which. To make a guaranteed identification, which one of the following tests should be used on the decompositions? (Assume that the closures of $$F$$ and $$G$$ are available).

GATE CSE 2002

$$R(A,B,C,D)$$ is a relation. Which of the following does not have a lossless-join, dependency preserving $$BCNF$$ decomposition?

GATE CSE 2001

Given the following relation instance
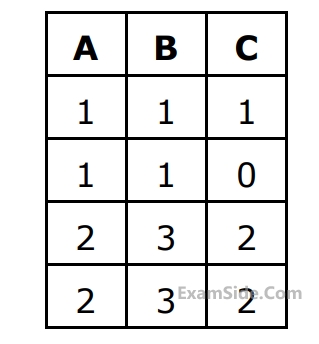
$$\eqalign{ & X\,\,\,\,\,Y\,\,\,\,\,Z \cr & \,\,1\,\,\,\,\,\,4\,\,\,\,\,\,2 \cr & \,\,1\,\,\,\,\,\,5\,\,\,\,\,\,3 \cr & \,\,1\,\,\,\,\,\,6\,\,\,\,\,\,3 \cr & \,\,3\,\,\,\,\,\,2\,\,\,\,\,\,2 \cr} $$

Which of the following functional dependencies are satisfied by the instance?

GATE CSE 2000

Consider the schema $$R = \left( {S\,\,T\,\,U\,\,V} \right)$$ and the dependencies $$S \to T,\,\,T \to U,\,\,U \to V$$ and $$V \to S$$ let $$R =$$ $$(R1$$ and $$R2)$$ be a decomposition such that $$R1 \cap R2 \ne \phi .$$ The decomposition is:

GATE CSE 1999

Consider the following database relations containing the attributes
Book–id
Subject–Category–of–book
Name–of–Author
Nationality–of–Author
With book–id as the primary key.
(a) What is the highest normal form satisfied by this relation?

(b) Suppose the attributes Book–title and Author–address are added to the relation, and the primary key is changed to {Name–of–Author, Book–title}, what will be the highest normal form satisfied by the relation?

GATE CSE 1998

Let $$R (a, b, c)$$ and $$S(d, e, f)$$ be two relations in which $$d$$ is the foreign key of $$S$$ that refers to the primary key of $$R.$$ Consider the following four operations $$R$$ and $$S$$
(a) Insert into $$R$$ (b) Insert into $$S$$
(c) Delete from $$R$$ (d) Delete from $$S$

Which of the following statements is true about the referential integrity constraint above?

GATE CSE 1997

For a database relation $$R(a,b,c,d),$$ where the domains of $$a, b, c, d$$ include only atomic values, only the following functional dependencies and those that can be inferred from them hold:
$$a \to c\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,b \to d$$
This relation is

GATE CSE 1997

(a) Consider the relation scheme $$R(A, B, C)$$ with the following functional dependencies:
$$\eqalign{ & A,B \to C \cr & \,\,\,\,\,\,C \to A \cr} $$
Show that the scheme $$R$$ is the Third Normal Form $$(3NF)$$ but not in Boyce-Code Normal Form $$(BCNF).$$

(b) Determine the minimal keys of relation $$R.$$

GATE CSE 1995