Software Engineering · Software Engineering · GATE CSE
Marks 1
Number of external inputs $$\left( {\rm I} \right) = 30$$
Number of external outputs $$\left( O \right) = 60$$
Number of external inquiries $$\left( E \right) = 23$$
Number of files $$(F) = 08$$
Number of external interfaces $$(N) = 02$$
It is given that the complexity weighting factors for $$I, O, E, F$$ and $$N$$ are $$4, 5, 4, 10$$ and $$7,$$ respectively. It is also given that, out of fourteen value adjustment factors that influence the development effort, four factors are not applicable, each of the other four factors have value $$3,$$ and each of the remaining factors have value $$4.$ The computed value of function point metric is _____________.
Match the following:
| List I | List II |
|---|---|
| (P) Condition coverage | (i) Black-box testing |
| (Q) Equivalence class partitioning | (ii) System testing |
| (R) Volume testing | (iii) White-box testing |
| (S) Alpha testing | (iv) Performance testing |
$$1)$$ Waterfall model
$$2)$$ Evolutionary model
$$3)$$ Component-based software engineering
$$4)$$ Spiral development
$$a)$$ Specifications can be developed incrementally
$$b)$$ Requirements compromises are inevitable
$$c)$$ Explicit recognition of risk
$$d)$$ Inflexible partitioning of the project into

Total cost of the project includes cost of development & maintenance. What is the $$LOC$$ for $${L_1}$$ for which the cost of the project using $${L_1}$$ is equal to the cost of the project using $${L_2}$$
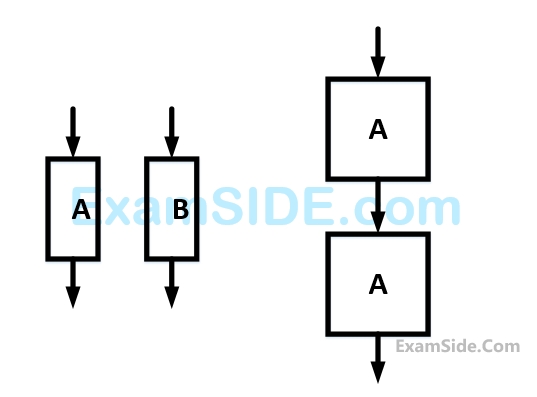
$${\rm I}.\,\,\,\,\,\,\,\,\,\,\,$$ Content coupling
$${\rm II}.\,\,\,\,\,\,\,\,\,$$ Common coupling
$${\rm III}.\,\,\,\,\,\,\,$$ Control coupling
$${\rm IV}.\,\,\,\,\,\,\,$$ Stamp coupling
$${\rm V}.\,\,\,\,\,\,\,\,\,$$ Data coupling
Coupling between modules can be ranked in the order of strongest (least desirable) to weakest (most desirable) as follows.
Marks 2

The values of McCabe’s Cyclomatic complexity of Program-$$X,$$ Program-$$Y,$$ and Program-$$Z$$ respectively are
while(first <= last)
{
if (array[middle] < search)
first = middle + 1;
else if (array[middle] == search)
found = TRUE;
else last = middle - 1;
middle = (first + last)/2;
}
if (first > last) notPresent = TRUE; $$\left\{ \, \right.$$ for (int $$i=0; i<5; i++$$)
for (int $$j=0; j<3; j++$$)
if ( $$A$$ [ $$i$$ ] $$==oldc$$ [ $$j$$ ] $$A$$ [ $$i$$ ]
$$=newc$$ [ $$j$$ ]; $$\left. \, \right\}$$
The procedure is tested with the following four test cases;
$$\eqalign{
& \left( 1 \right)\,\,\,oldc = ''abc'',\,\,newc\, = \,''dab'' \cr
& \left( 2 \right)\,\,\,oldc\, = \,''cdc'',\,\,newc\, = \,''bed'' \cr
& \left( 3 \right)\,\,\,oldc\, = \,''bca'',\,newc\, = \,''cda'' \cr
& \left( 4 \right)\,\,\,oldc\, = \,''abc'',\,newc\, = \,''bac'' \cr} $$
The tester now tests the program on all input strings of length five consisting of characters $$'a', 'b', 'c', 'd'$$ and $$'c'$$ with duplicates allowed. If the tester carries out this testing with four test cases given above, how many test cases will be able to capture the flaw?
$$\left\{ \, \right.$$ for (int $$i=0; i<5; i++$$)
for (int $$j=0; j<3; j++$$)
if ( $$A$$ [ $$i$$ ] $$==oldc$$ [ $$j$$ ] $$A$$ [ $$i$$ ]
$$=newc$$ [ $$j$$ ]; $$\left. \, \right\}$$
The procedure is tested with the following four test cases;
$$\eqalign{
& \left( 1 \right)\,\,\,oldc = ''abc'',\,\,newc\, = \,''dab'' \cr
& \left( 2 \right)\,\,\,oldc\, = \,''cdc'',\,\,newc\, = \,''bed'' \cr
& \left( 3 \right)\,\,\,oldc\, = \,''bca'',\,newc\, = \,''cda'' \cr
& \left( 4 \right)\,\,\,oldc\, = \,''abc'',\,newc\, = \,''bac'' \cr} $$
If array $$A$$ is made to hold the string $$''abcde'',$$ which of the above four test cases will be successful is exposing the flaw in this procedure?

$$i)$$ When coefficient $$a$$ is zero or irrespective of discriminate
$$ii)$$ When discriminate is positive.
$$iii)$$ When discriminate is zero
$$iv)$$ When discriminate is negative
Only in cases $$(ii)$$ & $$(iii)$$ the stored roots are valid Otherwise $$0$$ is stored in the roots the function returns $$0$$ when the roots are valid & - $$1$$ otherwise. The function also ensures root $$1$$ $$> =$$ root $$2.$$
int get QuadRoots(float a, float b, float c, float $${}^ * root1$$, float $${}^ * root2$$);
A software test engineer is assigned the job of doing block box testing. He comes up with the following test cases, many of which are redundant
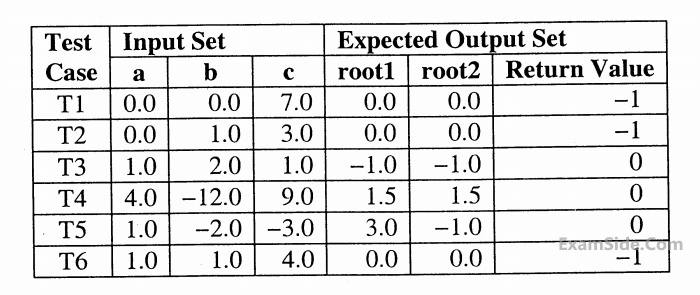
Which one of the following options provide the set of non-redundant tests using equivalence class partitioning approach from input perspective for black box testing?
begin
if $$\left( {a = \,\, = b} \right)\,\,\left\{ {S1;\,\,exit;} \right\}$$
else if $$\left( {c = \,\, = d} \right)\,\,\left\{ {S2;} \right\}$$
else $$\left\{ {S3;\,\,exit;} \right\}$$
$$S4;$$
end
The test cases $${T_1},\,{T_2},\,{T_3}\,\,\& \,{T_4}$$ given below are expressed in terms of the properties satisfied by the values of variables $$a, b, c$$ and $$d.$$ The exact values are not given.
$${T_1}:\,a,\,b,\,c\,\& \,d$$ are all equal
$${T_2}:\,a,\,b,\,c\,\& \,d$$ are all distinct
$${T_3}:\,a = b\,\,\,\& \,\,\,\,c\,!\, = \,d$$
$${T_4}:\,a! = b\,\,\,\& \,\,\,\,c\, = \,d$$
Which of the test suites given below ensures coverage of statements $${S_1},\,{S_2},\,{S_3}\,\,\& \,{S_4}$$ ?
$${\rm I}.\,\,\,\,\,\,$$ The content diagram should depict the system as a single bubble.
$${\rm II}.\,\,\,\,$$ External entities should be identified clearly at all levels of $$DFDs$$
$${\rm III}.\,\,$$ Control information should not be represented in $$DFD$$
$${\rm IV}.\,\,$$ A data store can be connected either to another data store or to an external
$$\,\,\,\,\,\,\,\,\,\,\,\,$$entity.
$${\rm I}.\,\,\,\,\,\,$$ The cyclomatic complexity of a module is equal to the maximum number of
$$\,\,\,\,\,\,\,\,\,\,\,$$linearly independent circuits in the graph.
$${\rm II}.\,\,\,$$ The cyclomatic complexity of a module is the number of decisions in the
$$\,\,\,\,\,\,\,\,\,\,$$module plus one, where a decision is effectively any conditional statement in
$$\,\,\,\,\,\,\,\,\,\,$$the module.
$${\rm III}\,$$ The cyclomatic complexity can also be used as a number of linearly
$$\,\,\,\,\,\,\,\,\,\,$$independent paths that should be tested during path coverage testing.