Parsing · Compiler Design · GATE CSE
Marks 1
Which ONE of the following statements is FALSE regarding the symbol table?
Which of the following statements is/are FALSE?
Which of the following is/are Bottom-Up Parser(s)?
Consider the following statements regarding the front-end and back-end of a compiler.
S1: The front-end includes phases that are independent of the target hardware.
S2: The back-end includes phases that are specific to the target hardware.
S3: The back-end includes phases that are specific to the programming language used in the source code.
Identify the CORRECT option.
Which one of the following statements is TRUE?
Consider the augmented grammar with {+, *, (, ), id} as the set of terminals.
S' $$\to$$ S
S $$\to$$ S + R | R
R $$\to$$ R * P | P
P $$\to$$ (S) | id
If I0 is the set of two LR(0) items {[S' $$\to$$ S.], [S $$\to$$ S. + R]}, then goto(closure(I0), +) contains exactly _________ items.
Consider the following statements.
S1 : Every SLR(1) grammar is unambiguous but there are certain unambiguous grammars that are not SLR(1).
S2 : For any context-free grammar, there is a parser that takes at most O(n3) time to parse a string of length n.
Which one of the following option is correct?
S $$ \to $$ aSB| d
B $$ \to $$ b
The number of reduction steps taken by a bottom-up parser while accepting the string aaadbbb is _______.
S → Aa
A → BD
B → b | ε
D → d | ε
Let a, b, d, and $ be indexed as follows:
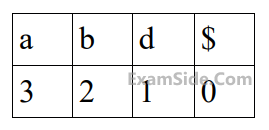
Compute the FOLLOW set of the non-terminal B and write the index values for the symbols in the FOLLOW set in the descending order. (For example, if the FOLLOW set is {a, b, d, $}, then the answer should be 3210)
| GROUP - 1 | GROUP - 2 |
|---|---|
| (P) Lexical analysis | (i) Leftmost derivation |
| (Q) Top down parsing | (ii) Type checking |
| (R) Semantic analysis | (iii) Regular expressions |
| (S) Runtime environments | (iv) Activation records |
| GROUP 1 | GROUP 2 |
|---|---|
| P. Lexical analysis | 1. Graph coloring |
| Q. Parsing | 2. DFA minimization |
| R. Register allocation | 3. Post-order traversal |
| S. Expression evaluation | 4. Production tree |
Consider the grammar defined by the following production rules, with two operators * and +
$$\eqalign{ & S \to T*P \cr & T \to U\,|\,T*U \cr & P \to Q + P\,|\,Q \cr & Q \to id \cr & U \to id \cr} $$Which one of the following is TRUE?
1) abaabaaabaa
2) aaaabaaaa
3) baaaaabaaaab
4) baaaaabaa
Consider the following grammar.
$$\eqalign{ & S \to S*E \cr & S \to E \cr & E \to F + E \cr & E \to F \cr & F \to id \cr} $$Consider the following LR(0) items corresponding to the grammar above.
$$\eqalign{ & (i)\,S \to S*.E \cr & (ii)\,E \to F. + E \cr & (iii)\,E \to F + .E \cr} $$Given the items above, which two of them will appear in the same set in the canonical sets-of-items for the grammar?
is not suitable for predictive-parsing because the grammar is
(i) object code generation
(ii) literals added to literal table
(iii) listing printed
(iv) address resolution of local symbols that occur in a two pass assembler respectively are
Marks 2
Given a Context-Free Grammar G as follows :
$S \rightarrow A a|b a c| d c \mid b d a$
$A \rightarrow d$
Which ONE of the following statements is TRUE?
Consider two grammars $G_1$ and $G_2$ with the production rules given below:
$G_1: S \rightarrow$ if $E$ then $S \mid$ if $E$ then $S$ else $S \mid a$
$$\mathrm{E} \rightarrow \mathrm{~b}$$
$G_2: S \rightarrow$ if $E$ then $S \mid M$
$E \rightarrow$ if $E$ then $M$ else $S \mid c$
$$\mathrm{E} \rightarrow \mathrm{~b}$$
where if, then, else, $a, b, c$ are the terminals.
Which of the following option(s) is/are CORRECT?
Which of the following statement(s) is/are TRUE while computing First and Follow during top down parsing by a compiler?
Consider the following context-free grammar where the start symbol is S and the set of terminals is {a,b,c,d}.
$ S \rightarrow AaAb \mid BbBa $
$ A \rightarrow cS \mid \epsilon $
$ B \rightarrow dS \mid \epsilon $
The following is a partially-filled LL(1) parsing table.
| a | b | c | d | $ | |
|---|---|---|---|---|---|
| S | S $\rightarrow$ AaAb | S $\rightarrow$ BbBa | (1) | (2) | |
| A | A $\rightarrow \epsilon$ | (3) | A $\rightarrow$ cS | ||
| B | (4) | B $\rightarrow \epsilon$ | B $\rightarrow$ dS |
Which one of the following options represents the CORRECT combination for the numbered cells in the parsing table?
Note: In the options, “blank” denotes that the corresponding cell is empty.
Consider the following augmented grammar, which is to be parsed with a SLR parser. The set of terminals is $\{ a, b, c, d, \, \#, \, @ \}$
$S' \rightarrow S$
$S \rightarrow SS \;|\; Aa \;|\; bAc \;|\; Bc \;|\; bBa$
$A \rightarrow d\#\#$
$B \rightarrow @$
Let $I_0 = \text{CLOSURE}( \{ S' \rightarrow \bullet S \} )$. The number of items in the set $GOTO(I_0, \, S)$ is __________.
Consider the following grammar $G$, with $S$ as the start symbol. The grammar $G$ has three incomplete productions denoted by (1), (2), and (3).
$$S \rightarrow d a T \mid \underline{\ (1)}$$
$$T \rightarrow a S \mid b T \mid \ \underline{(2)}$$
$$R \rightarrow \underline{(3)} \mid \epsilon$$
The set of terminals is $\{a, b, c, d, f\}$. The FIRST and FOLLOW sets of the different non-terminals are as follows.
FIRST($S$) = $\{c, d, f\}$, FIRST($T$) = $\{a, b, \epsilon\}$, FIRST($R$) = $\{c, \epsilon\}$
FOLLOW($S$) = FOLLOW($T$) = $\{c, f, \#\}$, FOLLOW($R$) = $\{f\}$
Which one of the following options CORRECTLY fills in the incomplete productions?
Consider the following augmented grammar with {#, @, <, >, a, b, c} as the set of terminals.
S' → S
S → S # cS
S → SS
S → S @
S → < S >
S → a
S → b
S → c
Let I0 = CLOSURE({S' → ∙ S}). The number of items in the set GOTO(GOTO(I0, <), <) is _______
Consider the following context-free grammar where the set of terminals is {a, b, c, d, f}.
S → d a T | R f
T → a S | b a T | ϵ
R → c a T R | ϵ
The following is a partially-filled LL(1) parsing table.

Which one of the following choices represents the correct combination for the numbered cells in the parsing table ("blank" denotes that the corresponding cell is empty)?
Rule 1 : P.i = A.i + 2, Q.i = P.i + A.i, and A.s = P.s + Q.s
Rule 2 : X.i = A.i + Y.s and Y.i = X.s + A.i
Which one of the following is TRUE?
S' → S
S → 〈L〉 | id
L → L,S | S
Let I0 = CLOSURE ({[S' → ●S]}). The number of items in the set GOTO (I0 , 〈 ) is: _____.

Which one of the following is correct for the given parse tree?
The grammars use D as the start symbol, and use six terminal symbols int ; id [ ] num.
| Grammar G1 | Grammar G2 |
|---|---|
| D → intL; | D → intL; |
| L → id[E | L → idE |
| E → num | E → E[num] |
| E → num][E | E → [num] |
Which of the grammars correctly generate the declaration mentioned above?
| Operator | Precedence | Associativity | Arity |
|---|---|---|---|
| + | High | Left | Binary |
| _ | Medium | Right | Binary |
| * | Low | Left | Binary |
The value of the expression $$2 - 5 + 1 - 7 * 3$$ in this language is _______________.
$$\eqalign{ & \,\,\,\,\,\,\,S \to \,\,\,\,\,\,\,F|H \cr & \,\,\,\,\,\,F \to \,\,\,\,\,\,\,p|c \cr & \,\,\,\,\,\,H \to \,\,\,\,\,\,\,d|c \cr} $$
where $$S, F$$ and $$H$$ are non-terminal symbols, $$p, d,$$ and $$c$$ are terminal symbols. Which of the following statement(s) is/are correct?
$$\,\,\,\,\,\,\,S1.\,\,\,\,\,\,\,LL\left( 1 \right)\,\,$$ can parse all strings that are generated using grammar $$G$$
$$\,\,\,\,\,\,\,S2.\,\,\,\,\,\,\,LR\left( 1 \right)\,\,$$ can parse all strings that are generated using grammar $$G$$
A canonical set of items is given below
$$\eqalign{ & S \to L. > R \cr & Q \to R. \cr} $$On input symbol < the set has
Consider the following two sets of LR(1) items of an LR(1) grammar.
$$\eqalign{ & X \to c.X,\,c/d\,\,\,\,\,\,\,\,X \to c.X,\$ \cr & X \to .cX,c/d\,\,\,\,\,\,\,\,X \to .cX,\$ \cr & X \to .d,c/d\,\,\,\,\,\,\,\,\,\,\,X \to .d,\$ \cr} $$Which of the following statements related to merging of the two sets in the corresponding LALR parser is/are FALSE?
1. Cannot be merged since look aheads are different.
2. Can be merged but will result in S-R conflict.
3. Can be merged but will result in R-R conflict.
4. Cannot be merged since goto on c will lead to two different sets.
Consider the grammar with non-terminals N = { S, C, S1 }, terminals T = { a, b, i, t, e }, with S as the start symbol, and the following set of rules:
$$\eqalign{ & S \to iCtS{S_1}\,|\,\,a \cr & {S_1} \to eS\,|\,\,\varepsilon \cr & C \to b \cr} $$The grammar is NOT LL(1) because:
P: Every regular grammar is LL(1)
Q: Every regular set has a LR(1) grammar
Consider the CFG with { S, A, B } as the non-terminal alphabet, { a, b } as the terminal alphabet, S as the start symbol and the following set of production rules:
$$\eqalign{ & S \to bA\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,S \to aB \cr & A \to a\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,B \to b \cr & A \to aS\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,B \to bS \cr & S \to bAA\,\,\,\,\,\,\,\,\,\,\,B \to aBB \cr} $$Which of the following strings is generated by the grammar?
Consider the CFG with { S, A, B } as the non-terminal alphabet, { a, b } as the terminal alphabet, S as the start symbol and the following set of production rules:
$$\eqalign{ & S \to bA\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,S \to aB \cr & A \to a\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,B \to b \cr & A \to aS\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,B \to bS \cr & S \to bAA\,\,\,\,\,\,\,\,\,\,\,B \to aBB \cr} $$For the correct answer strings to the previous question, how many derivation trees are there?
Consider the following grammar:
$$\eqalign{ & S \to FR \cr & R \to *S\,|\,\varepsilon \cr & F \to id \cr} $$In the predictive parser table, M, of the grammar the entries $$M\left[ {S,id} \right]$$ and $$M\left[ {R,\$ } \right]$$ respectively.
Which one of the following grammars generates the following language?
$$L = \left( {{a^i}{b^j}|i \ne j} \right)$$Consider the grammar
$$S \to \left( S \right)\,|\,a$$Let the number of states in SLR(1), LR(1) and LALR(1) parsers for the grammar be n1, n2 and n3 respectively.
The following relationship holds goodConsider the grammar
$$E \to E + n\,|\,E \times n\,|\,n$$For a sentence n + n × n, the handles in the right-sentential form of the reduction are
Consider the following expression grammar. The semantic rules for expression calculation are stated next to each grammar production.
$$\eqalign{ & E \to number\,\,\,\,\,E.val = number.val \cr & \,\,\,\,\,\,\,\,\,\,\,|E\,\,' + '\,\,E\,\,\,\,\,\,{E^{\left( 1 \right)}}.val = {E^{\left( 2 \right)}}.val + {E^{\left( 3 \right)}}.val \cr & \,\,\,\,\,\,\,\,\,\,\,|\,E\,\,' \times '\,\,E\,\,\,\,\,\,\,{E^{\left( 1 \right)}}.val = {E^{\left( 2 \right)}}.val \times {E^{\left( 3 \right)}}.val \cr} $$The above grammar and the semantic rules are fed to a yacc tool (which is an LALR (1) parser generator) for parsing and evaluating arithmetic expressions. Which one of the following is true about the action of yacc for the given grammar?
Consider the following expression grammar. The semantic rules for expression calculation are stated next to each grammar production.
$$\eqalign{ & E \to number\,\,\,\,\,E.val = number.val \cr & \,\,\,\,\,\,\,\,\,\,\,|E\,\,' + '\,\,E\,\,\,\,\,\,{E^{\left( 1 \right)}}.val = {E^{\left( 2 \right)}}.val + {E^{\left( 3 \right)}}.val \cr & \,\,\,\,\,\,\,\,\,\,\,|\,E\,\,' \times '\,\,E\,\,\,\,\,\,\,{E^{\left( 1 \right)}}.val = {E^{\left( 2 \right)}}.val \times {E^{\left( 3 \right)}}.val \cr} $$Assume the conflicts in the previous question are resolved and an LALR(1) parser is generated for parsing arithmetic expressions as per the given grammar. Consider an expression
3 × 2 + 1.
What precedence and associativity properties does the generated parser realize?
Which of the following grammar rules violate the requirements of an operator grammar? P, Q, R are nonterminals, and r, s, t are terminals.
$$\eqalign{ & 1.\,P \to QR \cr & 2.\,P \to QsR \cr & 3.\,P \to \varepsilon \cr & 4.\,P \to QtRr \cr} $$Consider the grammar with the following translation rules and E as the start symbol.
$$\eqalign{ & E \to {E_1}\# T\,\,\left\{ {E.value = {E_1}.value*T.value} \right\} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,|T\,\,\,\,\,\,\,\,\,\,\,\,\left\{ {E.value = T.value} \right\} \cr & T \to {T_1}\& F\,\,\,\left\{ {T.value = {T_1}.value*F.value} \right\} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,|\,F\,\,\,\,\,\,\,\,\,\,\,\left\{ {T.value = F.value} \right\} \cr & F \to num\,\,\,\,\,\,\,\left\{ {F.value = num.value} \right\} \cr} $$Compute E.value for the root of the parse tree for the expression:
2 # 3 & 5 # 6
& 4.
Consider the grammar shown below.
$$\eqalign{ & S \to CC \cr & C \to cC\,|\,d \cr} $$This grammar is
Consider the translation scheme shown below
$$\eqalign{ & S \to TR \cr & R \to + T\left\{ {pr{\mathop{\rm int}} (' + ');} \right\}\,R\,|\,\varepsilon \cr & T \to num\,\left\{ {pr{\mathop{\rm int}} (num.val);} \right\} \cr} $$Here num is a token that represents an integer and num.val represents the corresponding integer value. For an input string '9 + 5 + 2', this translation scheme will print
Consider the grammar shown below
$$\eqalign{ & S \to iEtSS'\,|\,\,a \cr & S' \to eS\,|\,\,\varepsilon \cr & E \to b \cr} $$In the predictive parse table, $$M$$, of this grammar, the entries $$M\left[ {S',e} \right]$$ and $$M\left[ {S',\phi } \right]$$ respectively are
A shift reduce parser carries out the actions specified within braces immediately after reducing with the corresponding rule of grammar.
$$\eqalign{ & S \to xxW\,\left\{ {pr{\mathop{\rm int}} \,'1'} \right\} \cr & S \to y\,\left\{ {pr{\mathop{\rm int}} \,'2'} \right\} \cr & W \to Sz\,\left\{ {pr{\mathop{\rm int}} \,'3'} \right\} \cr} $$What is the translation of xxxxyzz using the syntax directed translation scheme described by the above rules?