Searching and Sorting · Algorithms · GATE CSE

An array of 25 distinct elements is to be sorted using quicksort. Assume that the pivot element is chosen uniformly at random. The probability that th...

Assume that the algorithms considered here sort the input sequences in ascending order. If the input is already in ascending order, which of the follo...

The worst case running times of Insertion sort, Merge sort and Quick sort, respectively, are:

Which one of the following is the recurrence equation for the worst case time complexity of the Quicksort algorithm for sorting n ( $$ \ge 2$$ ) numb...

An unordered list contains $$n$$ distinct elements. The number of comparisons to find an element in this list that is neither maximum nor minimum is

Consider the following array of elements. $$\,\,\,\,\,\,\,\,$$$$〈89, 19, 50, 17, 12, 15, 2, 5, 7, 11, 6, 9, 100〉$$ The minimum number of interchanges ...

A priority queue is implemented as a Max-Heap. Initially, it has 5 elements. The level-order traversal of the heap is: 10, 8, 5, 3, 2. Two new element...

A max-heap is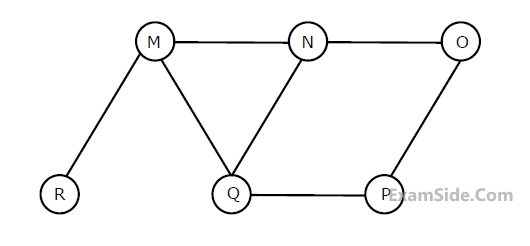 a heap where the value of each parent is greater than or equal to the value of its children. Which of the following is a max-heap?

What is the number of swaps required to sort n elements using selection sort, in the worst case?

The most efficient algorithm for finding the number of connected components in an undirected graph on n vertices and m edges has time complexity

The Breadth First Search algorithm has been implemented using the queue data structure. One possible order of visiting the nodes of the following grap...

Consider the DAG with $$V = \{1,2,3,4,5,6\}$$, shown below. Which of the following is NOT a topological ordering?...

Which of the following sorting algorithms has the lowest worst-case complexity?

In a binary max heap containing n numbers, the smallest element can be found in time

Which one of the following in place sorting algorithms needs the minimum number of swaps?

An element in an array X is called a leader if it is greater than all elements to the right of it in X. The best algorithm to find all leaders in an a...

The tightest lower bound on the number of comparisons, in the worst case, for comparison-based sorting is of the order of

In a heap with n elements with the smallest element at the root, the 7th smallest element can be found in time

Consider any array representation of an n element binary heap where the elements are stored from index 1 to index n of the array. For the element stor...

Suppose we want to arrange the n numbers stored in any array such that all negative values occur before all positive ones. Minimum number of exchanges...

The number of articulation points of the following graph is ...

Give the correct matching for the following pairs: Group - 1 (A) $${\rm O}(\log n)$$ (B) $${\rm O}(n)$$ (C) $${\rm O}(n\log n)$$ (D) $${\rm O}({n^2})$...

The correct matching for the following pairs is .tg {border-collapse:collapse;border-spacing:0;border:none;} .tg td{font-family:Arial, sans-serif;fo...

Consider the following array. 23 32 45 69 72 73 89 97 ...

The number of possible min-heaps containing each value from $$\left\{ {1,2,3,4,5,6,7} \right\}$$ exactly once is _____.

A complete binary min-heap is made by including each integer in $$[1,1023]$$ exactly once. The depth of a node in the heap is the length of the path f...

An operator $$delete(i)$$ for a binary heap data structure is to be designed to delete the item in the $$i$$-th node. Assume that the heap is implemen...

Consider a max heap, represented by the array: 40, 30, 20, 10, 15, 16, 17, 8, 4. .tg {border-collapse:collapse;border-spacing:0;} .tg td{font-family...

Suppose you are provided with the following function declaration in the C programming language. int partition(int a[], int n); The function treats th...

Assume that a mergesort algorithm in the worst case takes $$30$$ seconds for an input of size $$64.$$ Which of the following most closely approximates...

Consider a binary max-heap implemented using an array. Which one of the following array represents a binary max-heap?

Consider a binary max-heap implemented using an array. What is the content of the array {25, 14, 16, 13, 10, 8, 12} after two delete operations?

We have a binary heap on n elements and wish to insert n more elements (not necessarily one after another) into this heap. The total time required for...

Consider the process of inserting an element into a Max Heap, where the Max Heap is represented by an array. Suppose we perform a binary search on the...

A 3-ary max heap is like a binary max heap, but instead of 2 children, nodes have 3 children. A 3-ary heap can be represented by an array as follows: ...

Given two arrays of numbers a1,......,an and b1,......, bn where each number is 0 or 1, the fastest algorithm to find the largest span (i, j) such tha...

A 3-ary max heap is like a binary max heap, but instead of 2 children, nodes have 3 children. A 3-ary heap can be represented by an array as follows: ...

Suppose there are $$\lceil \log n \rceil$$ sorted lists of $$\left\lfloor {{n \over {\log n}}} \right\rfloor $$ elements each. The time complexity of ...

Let G(V, E) an undirected graph with positive edge weights. Dijkstra's single-source shortest path algorithm can be implemented using the binary heap ...

The elements 32, 15, 20, 30, 12, 25, 16, are inserted one by one in the given order into a max Heap. The resultant max Heap is

If T1 = O(1), give the correct matching for the following pairs: List - I (M) Tn = Tn - 1 + n (N) Tn = Tn/2 + n (O) Tn = Tn/2 + nlog n (P) Tn = Tn - 1...

The minimum number of interchanges needed to convert the array 89, 19, 40, 17, 12, 10, 2, 5, 7, 11, 6, 9, 70 into a heap with the maximum element at t...

The average number of key comparisons done on a successful sequential search in list of length n is

Which one of the following statements is false?

Following algorithm(s) can be used to sort n integers in the range [1....... n3] in O(n) time

Minimum number of comparisons required to sort 5 elements

Match the pairs in the following: List - I (a) Straseen's matrix multiplication algorithm (b) Kruskal's minimum spanning tree algorithm (c) Bioconnect...

Match the pairs in the following: List - I (a) Heap construction (b) Constructing hash table witn linear probing (c) AVL Tree construction (d) Digital...