Numerical Ability · General Aptitude · GATE CSE
Marks 1
If $P e^x=Q e^{-x}$ for all real values of $x$, which one of the following statements is true?
Let $p_1$ and $p_2$ denote two arbitrary prime numbers. Which one of the following statements is correct for all values of $p_1$ and $p_2$ ?
The average marks obtained by a class in an examination were calculated as 30.8 . However, while checking the marks entered, the teacher found that the marks of one student were entered incorrectly as 24 instead of 42 . After correcting the marks, the average becomes 31.4. How many students does the class have?
Two wizards try to create a spell using all the four elements, water, air, fire, and earth. For this, they decide to mix all these elements in all possible orders. They also decide to work independently. After trying all possible combinations of elements, they conclude that the spell does not work.
How many attempts does each wizard make before coming to this conclusion, independently?
In an engineering college of 10,000 students, 1,500 like neither their core branches nor other branches. The number of students who like their core branches is 1/4th of the number of students who like other branches. The number of students who like both their core and other branches is 500.
The number of students who like their core branches is
For positive non-zero real variables $x$ and $y$, if
$\ln \left( \frac{x + y}{2} \right) = \frac{1}{2} [ \ln (x) + \ln (y) ]$
then, the value of $\frac{x}{y} + \frac{y}{x}$ is
In the sequence 6, 9, 14, $x$, 30, 41, a possible value of $x$ is
Consider the following sample of numbers:
9, 18, 11, 14, 15, 17, 10, 69, 11, 13
The median of the sample is
The number of coins of ₹1, ₹5, and ₹10 denominations that a person has are in the ratio 5:3:13. Of the total amount, the percentage of money in ₹5 coins is
If two distinct non-zero real variables $x$ and $y$ are such that $(x + y)$ is proportional to $(x - y)$ then the value of $\frac{x}{y}$
For positive non-zero real variables $p$ and $q$, if
$\log \left(p^2 + q^2\right) = \log p + \log q + 2 \log 3$,
then, the value of $\frac{p^4 + q^4}{p^2 q^2}$ is
A series of natural numbers $$F_1,F_2,F_3,F_4,F_5,F_6,F_7,\,.....$$ obeys $$F_{n+1}=F_n+F_{n-1}$$ for all integers $$n\ge2$$.
If $$F_6=37$$, and $$F_7=60$$, then what is $$F_1$$ ?
A function y(x) is defined in the interval [0, 1] on the x-axis as
$$y(x) = \left\{ \matrix{ 2\,if\,0 \le x < {1 \over 3} \hfill \cr 3\,if\,{1 \over 3} \le x < {3 \over 4} \hfill \cr 1\,if\,{3 \over 4} \le x < 1 \hfill \cr} \right.$$
Which one of the following is the area under the curve for the interval [0, 1] on the x-axis?
Let r be a root of the equation x2 + 2x + 6 = 0. Then the value of the expression (r + 2) (r + 3) (r + 4) (r + 5) is
Among the options below, an acceptable value for the total number of students in the class is :

Choose the correct expression for $$f(x)$$ given in the graph.
Marks 2
Which one of the following options is correct for the given data in the table?
| Iteration ($i$) | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| Input ($I$) | 20 | $-$4 | 10 | 15 |
| Output ($X$) | 20 | 16 | 26 | 41 |
| Output ($Y$) | 20 | $-$80 | $-$800 | $-$12000 |
In the given figure, PQRS is a square of side 2 cm and PLMN is a rectangle. The corner L of the rectangle is on the side QR. Side MN of the rectangle passes through the corner S of the square.
What is the area (in $\mathrm{cm}^2$ ) of the rectangle PLMN?
Note: The figure shown is representative

In the diagram, the lines QR and ST are parallel to each other. The shortest distance between these two lines is half the shortest distance between the point $P$ and line QR. What is the ratio of the area of the triangle PST to the area of the trapezium SQRT?
Note: The figure shown is representative.

A fair six-faced dice, with the faces labelled ' 1 ', ' 2 ', ' 3 ', ' 4 ', ' 5 ', and ' 6 ', is rolled thrice. What is the probability of rolling ' 6 ' exactly once?
A shop has 4 distinct flavors of ice-cream. One can purchase any number of scoops of any flavor. The order in which the scoops are purchased is inconsequential. If one wants to purchase 3 scoops of ice-cream, in how many ways can one make that purchase?
A person sold two different items at the same price. He made 10% profit in one item, and 10% loss in the other item. In selling these two items, the person made a total of
The pie charts depict the shares of various power generation technologies in the total electricity generation of a country for the years 2007 and 2023.
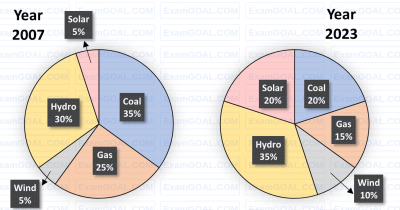
The renewable sources of electricity generation consist of Hydro, Solar and Wind. Assuming that the total electricity generated remains the same from 2007 to 2023, what is the percentage increase in the share of the renewable sources of electricity generation over this period?
A rectangular paper sheet of dimensions 54 cm × 4 cm is taken. The two longer edges of the sheet are joined together to create a cylindrical tube. A cube whose surface area is equal to the area of the sheet is also taken.
Then, the ratio of the volume of the cylindrical tube to the volume of the cube is
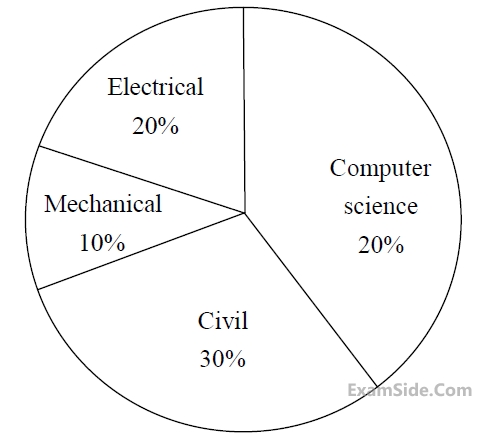
The pie chart presents the percentage contribution of different macronutrients to a typical 2,000 kcal diet of a person.
Macronutrient energy contribution

The typical energy density (kcal/g) of these macronutrients is given in the table:
| Macronutrient | Energy density (kcal/g) |
|---|---|
| Carbohydrates | 4 |
| Proteins | 4 |
| Unsaturated fat | 9 |
| Saturated fat | 9 |
| Trans fat | 9 |
The total fat (all three types), in grams, this person consumes is
A rectangular paper of 20 cm × 8 cm is folded 3 times. Each fold is made along the line of symmetry, which is perpendicular to its long edge. The perimeter of the final folded sheet (in cm) is
The least number of squares to be added in the figure to make AB a line of symmetry is

Consider two functions of time (t),
$$f(t)=0.01\,t^2$$
$$g(t)=4\,t$$
where $$0 < t < \infty$$.
Now consider the following two statements :
(i) For some $$t > 0,g(t) > f(t)$$.
(ii) There exists a $$T$$, such that $$f(t) > g(t)$$ for all $$t > T$$.
Which one of the following options is TRUE?
$$f(x)$$ and $$g(y)$$ are functions of x and y, respectively, and $$f(x)=g(y)$$ for all real values of x and y. Which one of the following options is necessarily TRUE for al x and y?
A box contains five balls of same size and shape. Three of them are green coloured balls and two of them are orange coloured balls. Balls are drawn from the box one at a time. If a green ball is drawn, it is not replaced. If an orange ball is drawn, it is replaced with another orange ball.
First ball is drawn. What is the probability of getting an orange ball in the next draw?
The total number of students in all the three classes in the beginning was :
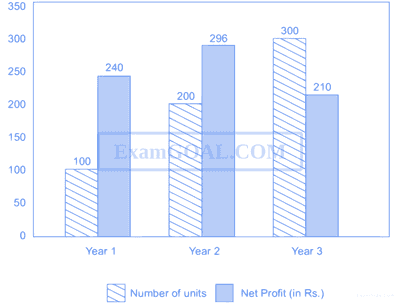
The number of units of a product sold in three different years and the respective net profits are presented in the figure above. The cost/unit in year 3 was Rs. 1, which was half the cost/unit in year 2. The cost/unit in year 3 was one-third of the cost/unit in year 1. Taxes were paid on the selling price at 10%, 13% and 15% respectively for the three years. Net profit is calculated as the difference between the selling price and the sum of cost and taxes paid in that year.
The ratio of the selling price in Year 2 to the selling price in Year 3 is _______
The probability that at least two chocolates are identical is ________.
| Items | Cost | Profit% | Marked price |
|---|---|---|---|
| P | 5400 | - | 5860 |
| Q | - | 25 | 10000 |
Details of prices of two items P and Q are presented in the above table. The ratio of cost of item P to cost of item Q is 3 : 4. Discount is calculated as the difference between the marked price and the selling price. The profit percentage is calculated as the ratio of the difference between selling price and cost, to the cost
(Profit% = $${{Selling\,price - Cost} \over {Cost}} \times 100$$).
The discount on item Q, as a percentage of its marked price, is ________.
| Quarter \ Product | Elegance | Smooth | Soft | Executive |
|---|---|---|---|---|
| Q1 | 27300 | 20009 | 17602 | 9999 |
| Q2 | 25222 | 19392 | 18445 | 8942 |
| Q3 | 28976 | 22429 | 19544 | 10234 |
| Q4 | 21012 | 18229 | 16595 | 10109 |
Which product contributes the greatest fraction to the revenue of the company in that year?
$$\left( I \right)\,p + m + c = {{27} \over {20}}$$
$$\left( {II} \right)\,p + m + c = {{13} \over {20}}$$
$$\left( {III} \right)\,\left( p \right) \times \left( m \right) \times \left( c \right) = {1 \over {10}}$$
The number of students in a class who have answered correctly, wrongly, or not attempted each question in an exam, are listed in the table below. The marks for each question are also listed. There is no negative or partial marking.
| Q No | Marks | Answered Correctly |
Answered Wrongly |
Not Attempted |
|---|---|---|---|---|
| 1 | 2 | 21 | 17 | 6 |
| 2 | 3 | 15 | 27 | 2 |
| 3 | 1 | 11 | 29 | 4 |
| 4 | 2 | 23 | 18 | 3 |
| 5 | 5 | 31 | 12 | 1 |
What is the average of the marks obtained by the class in the examination?