Graphs · Data Structures · GATE CSE

Marks 1

Which of the following statements regarding Breadth First Search (BFS) and Depth First Search (DFS) on an undirected simple graph G is/are TRUE?

GATE CSE 2025 Set 2

Consider the following undirected graph with edge weights as shown:

The number of minimum-weight spanning trees of the graph is ______

GATE CSE 2021 Set 1

Consider the following directed graph:

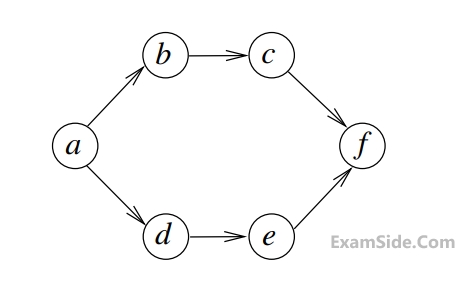
The number of different topological orderings of the vertices of the graph is ________________.

GATE CSE 2016 Set 1

Breadth First Search $$(BFS)$$ is started on a binary tree beginning from the root vertex. There is a vertex $$t$$ at a distance four from the root. If t is the $$n$$-th vertex in this $$BFS$$ traversal, then the maximum possible value of $$n$$ is ___________.

GATE CSE 2016 Set 2

Suppose depth first search is executed on the graph below starting at some unknown vertex. Assume that a recursive call to visit a vertex is made only after first checking that the vertex has not been visited earlier. Then the maximum possible recursion depth (including the initial call) is _________.

GATE CSE 2014 Set 3

Let G be a graph with n vertices and m edges. What is the tightest upper bound on the running time of Depth First Search on G, when G is represented as an adjacency matrix?

GATE CSE 2014 Set 1

Consider the tree arcs of a BFS traversal from a source node W in an unweighted, connected, undirected graph. The tree T formed by the tree arcs is a data structure for computing

GATE CSE 2014 Set 2

In a depth-first traversal of a graph G with n vertices,k edges are marked as tree edges. The number of connected components in G is

GATE CSE 2004

Consider the following graph among the following sequences
I. a b e g h f
II. a b f e h g
III. a b f h g e
IV. a f g h b e

What are depth first traversals of the above graph?

GATE CSE 2003

Marks 2

Consider the following algorithm someAlgo that takes an undirected graph $G$ as input. someAlgo ( $G$ )

1. Let $v$ be any vertex in $G$. Run BFS on $G$ starting at $v$. Let $u$ be a vertex in $G$ at maximum distance from $v$ as given by the BFS.

2. Run BFS on $G$ again with $u$ as the starting vertex. Let $z$ be the vertex at maximum distance from $u$ as given by the BFS.

3. Output the distance between $u$ and $z$ in $G$.

The output of someAlgo( $T$ ) for the tree shown in the given figure is $\qquad$ . (Answer in integer)

GATE CSE 2025 Set 2

Let $G(V, E)$ be an undirected and unweighted graph with 100 vertices. Let $d(u, v)$ denote the number of edges in a shortest path between vertices $u$ and $v$ in $V$. Let the maximum value of $d(u, v), u, v \in V$ such that $u \neq v$, be 30 . Let $T$ be any breadth-first-search tree of $G$. Which ONE of the given options is CORRECT for every such graph $G$ ?

GATE CSE 2025 Set 1

Let G be a directed graph and T a depth first search (DFS) spanning tree in G that is rooted at a vertex v. Suppose T is also a breadth first search (BFS) tree in G, rooted at v. Which of the following statements is/are TRUE for every such graph G and tree T?

GATE CSE 2024 Set 1

Let G = (V, E) be a directed, weighted graph with weight function w: E $$ \to $$ R. For some function f: V $$ \to $$ R, for each edge (u, v) $$ \in $$ E, define w'(u, v) as w(u, v) + f(u) - f(v).

Which one of the options completes the following sentence so that it is TRUE?
“The shortest paths in G under w are shortest paths under w’ too, _______”.

GATE CSE 2020

Let $$G$$ be a simple undirected graph. Let $${T_D}$$ be a depth first search tree of $$G.$$ Let $${T_B}$$ be a breadth first search tree of $$G.$$ Consider the following statements.

$$(I)$$ No edge of $$G$$ is a cross edge with respect to $${T_D}.$$ ($$A$$ cross edge in $$G$$ is between
$$\,\,\,\,\,\,\,\,$$ two nodes neither of which is an ancestor of the other in $${T_D}.$$)
$$(II)$$ For every edge $$(u,v)$$ of $$G,$$ if $$u$$ is at depth $$i$$ and $$v$$ is at depth $$j$$ in $${T_B}$$, then
$$\,\,\,\,\,\,\,\,\,\,\,$$ $$\left| {i - j} \right| = 1.$$

Which of the statements above must necessarily be true?

GATE CSE 2018

Let $$G$$ be a graph with $$100!$$ vertices, with each vertex labelled by a distinct permutation of the numbers $$1,2, … , 100.$$ There is an edge between vertices $$u$$ and $$v$$ if and only if the label of $$u$$ can be obtained by swapping two adjacent numbers in the label of $$v.$$ Let $$𝑦$$ denote the degree of a vertex in $$G,$$ and $$𝑧$$ denote the number of connected components in $$G.$$ Then, $$𝑦 + 10𝑧 =$$ _____.

GATE CSE 2018

In an adjacency list representation of an undirected simple graph $$G = (V,E),$$ each edge $$(u, v)$$ has two adjacency list entries: $$[v]$$ in the adjacency list of $$u,$$ and $$[u]$$ in the adjacency list of $$v.$$ These are called twins of each other. A twin pointer is a pointer from an adjacency list entry to its twin. If $$|E| = m$$ and $$|V| = n,$$ and the memory size is not a constraint, what is the time complexity of the most efficient algorithm to set the twin pointer in each entry in each adjacency list?

GATE CSE 2016 Set 2

Let $$G$$ be a connected undirected graph of $$100$$ vertices and $$300$$ edges. The weight of a minimum spanning tree of $$G$$ is $$500.$$ When the weight of each edge of $$G$$ is increased by five, the weight of a minimum spanning tree becomes ________.

GATE CSE 2015 Set 3

Let G = (V, E) be a simple undirected graph, and s be a particular vertex in it called the source. For $$x \in V$$, let d(x) denote the shortest distance in G from s to x. A breadth first search (BFS) is performed starting at s. Let T be the resultant BFS tree. If (u, v) is an edge of G that is not in T, then which one of the following CANNOT be the value of $$d\left( u \right) - d\left( v \right)$$?

GATE CSE 2015 Set 1

Let G be a weighted graph with edge weights greater than one and G' be the graph constructed by squaring the weights of edges in G. Let T and T' be the minimum spanning trees of G and G' respectively, with total weights t and t'. Which of the following statements is TRUE?

GATE CSE 2012